要在国际象棋棋盘中放八个皇后,使任意两个皇后都不能互相吃,皇后能吃同一行、同一列,同一对角线上(两个方向的对角线)的任意棋子。现在给一个整数n(n<=92),输出前n种的摆法。
输入一个整数n。
输出共n行。
每行8个数,表示每行所放的列号,每个数输出占4列。
3
1 5 8 6 3 7 2 4
1 6 8 3 7 4 2 5 1 7 4 6 8 2 5 3
思路:DFS,把每一个格子试一次。
提示:
确定两个棋子在不在统同一行,同一列,同一对角线的方法:
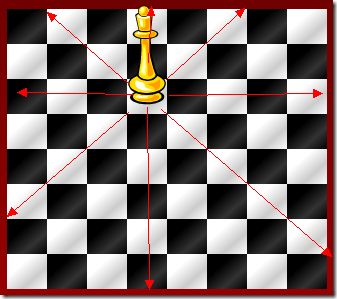
如下图,如果两个棋子在同一行,则i1=i2;
如果两个棋子在同一行列,则j1=j2;
如果两个棋子在同对角线,则i1+j1=i2+j2;

不多说了,上代码:

#include<bits/stdc++.h> using namespace std; int a[9],b[17],c[17],d[9],n,sum,m;//a[9],b[9],直线, c[17],d[17],对角线 void print(){ for(int i=1;i<=n;i++)printf("%4d",d[i]); cout<<endl; } void search(int row){//DFS if(row>n){//如果放满了就打印(print函数) sum++; if(sum<=m)print(); return;//返回 } for(int i=1;i<=n;i++){ if(a[i]==0 && b[row+i]==0 && c[row-i+7]==0){ a[i]=1; b[row+i]=1; c[row-i+7]=1;//放棋子 d[row]=i;//记录 search(row+1);//递归 a[i]=0; b[row+i]=0; c[row-i+7]=0;//恢复 } } } int main(){ n=8;//八皇后,故n=8 cin>>m; search(1); return 0; }
原文:https://www.cnblogs.com/YFbing/p/9588988.html