是一棵二叉树,任何节点的值一定大于其左子树中每一个节点的值,小于其右子树每一个节点的值
一棵二叉搜索树,任何节点的左子树高度和右子树高度最多相差1,严格平衡
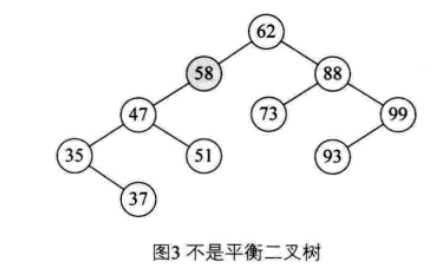
节点58左子树高度3,右子树高度0,相差3,所以不是平衡二叉树
节点结构
data、bf(平衡因子=左子树高度-右子树高度)、left指针、right指针
节点插入后,某节点X的左子树和右子树高度的差变成了2,破坏了平衡,可分为四种情况:
1.外侧插入:左左——插入点位于X左子节点的左子树
2.外侧插入:右右——插入点位于X右子节点的右子树
3.内侧插入:左右——插入点位于X左子节点的右子树
4.内侧插入:右左——插入点位于X右子节点的左子树
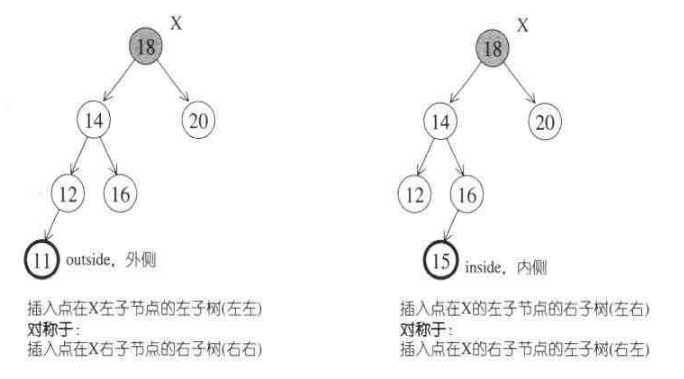
对于外侧插入,采用单旋转修正:左左(右单旋),右右(左单旋);
对于内侧插入,采用双旋转(两次单旋转)修正:左右(左单旋+右单旋),右左(右单旋+左单旋)
查找、插入、删除:O(logn)
是一棵二叉搜索树,确保最长路径不大于两倍的最短路径的长度,近似于平衡,且满足5个规则:
1.每个节点要么是红色,要么是黑色
2.根节点必为黑色
3.如果某个节点为红色,其儿子节点必须为黑色
4.任何一个节点至NULL的任何路径,所含黑色节点的数目相同
5.NULL视为黑色
规则4导致新增节点必须为红色,进而根据规则3,新增节点的父节点又必须为黑色,但是又需要根据二叉搜索树的规则来添加新增节点,所以可能会引发矛盾。此时,就需要调整颜色并旋转来修正
color(枚举型)、key、value、left指针、right指针、parent指针(红黑树的各种操作经常要上溯到父节点)
查找、插入、删除:O(logn)
未完待续
原文:https://www.cnblogs.com/Joezzz/p/9610861.html