一、微积分
1夹逼定理
通俗的讲:A≤B≤C
当求极限时,存在A=C,则说明B也等于A和C
案例1: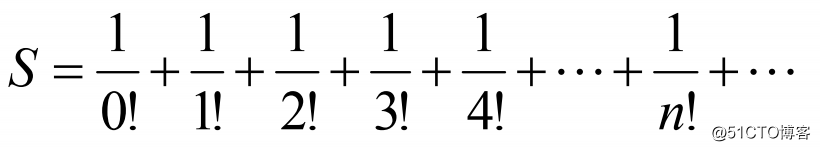
案例2:
2 两个重要极限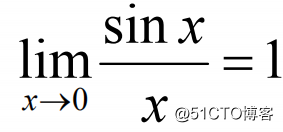
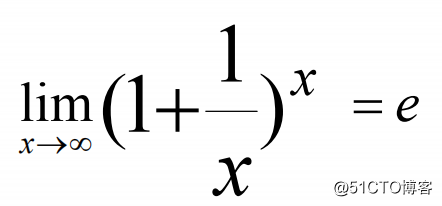
3 导数
通俗的讲就是曲线的斜率
二阶导数是斜率变化快慢的反应,表征曲线的凹凸性
常用的函数的导数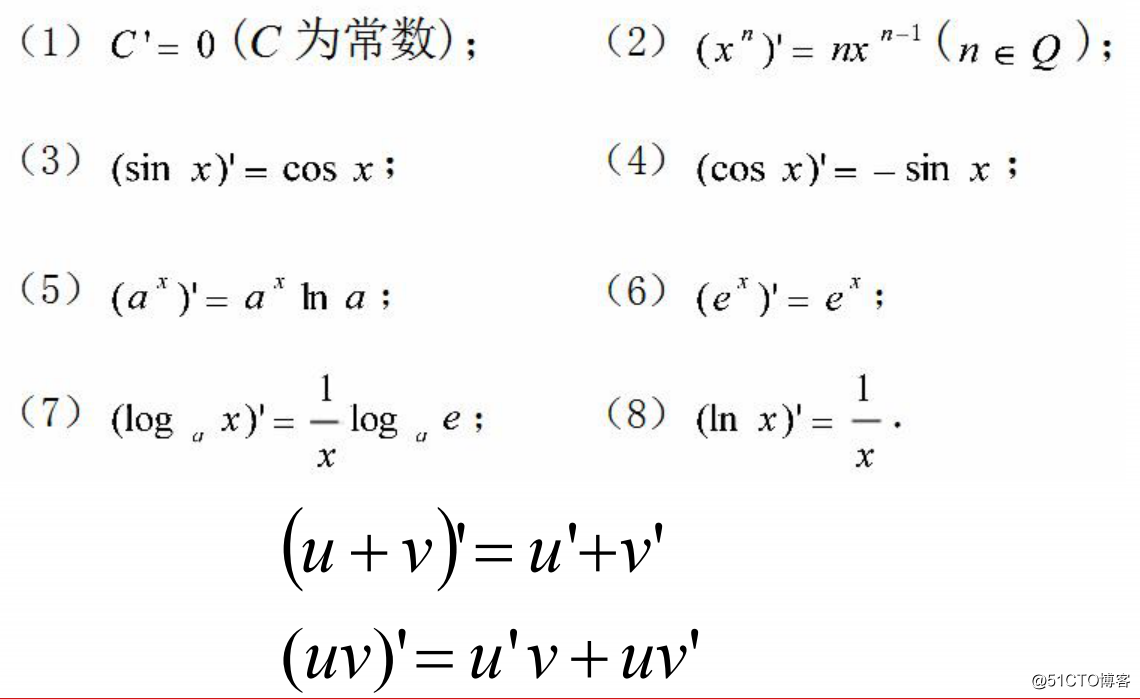
案例1:
求幂指函数的套路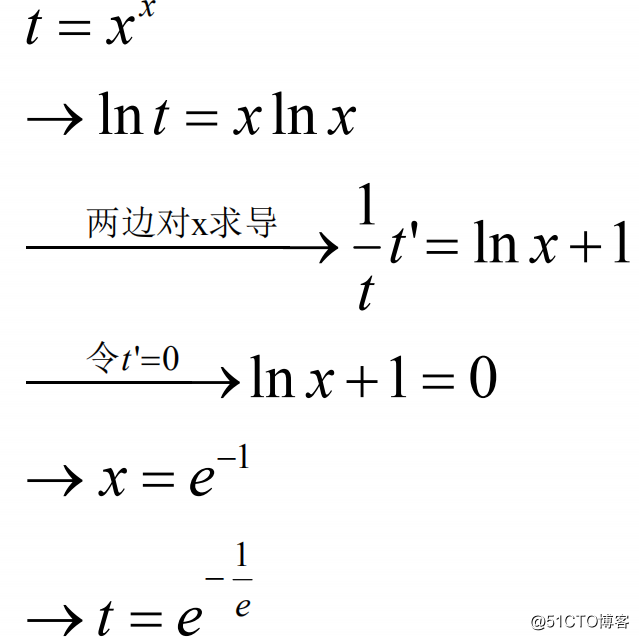
===重要公式之,泰勒公式: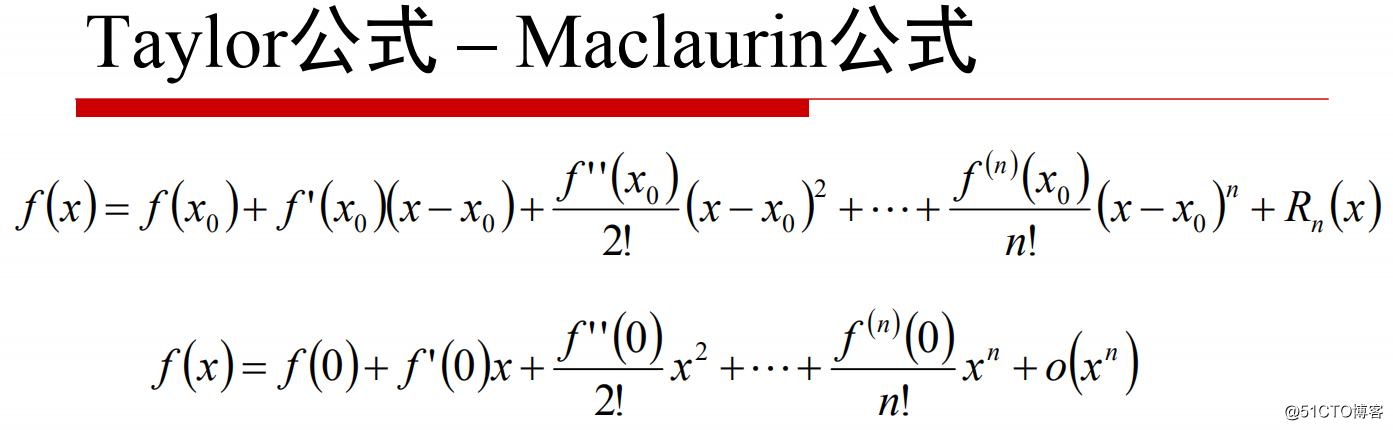
简单应用:
4 方向导数和梯度函数
(1)方向导数:如果函数z=f(x,y)在点P(x,y)是可微分的,那么,函数在该点沿任一方向L的方向导数都存在,且有: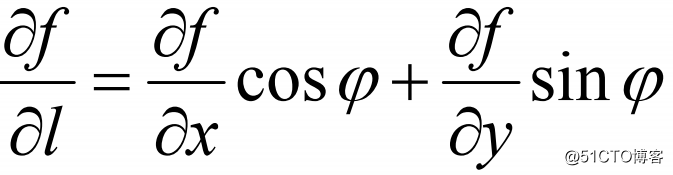
其中,ψ为x轴到方向L的转角
(2)梯度函数:
设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则对于每一个点P(x,y)∈D,向量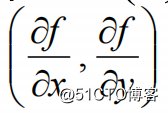
为函数z=f(x,y)在点P的梯度,记做gradf(x,y)
? 梯度的方向是函数在该点变化最快的方向
? 考虑一座解析式为H(x,y)的山。在(x0,y0)点的梯度是在
该点坡度最陡的方向。
? 梯度下降法
5 凸函数和凹函数
定理:f(x)在区间[a,b]上连续,在(a,b)内二阶
可导,那么:
? 若f’’(x)>0,则f(x)是凸的;
? 若f’’(x)<0,则f(x)是凹的;
应用案例:
设p(x)、q(x)是在X中取值的两个概率分布,给定如下定义式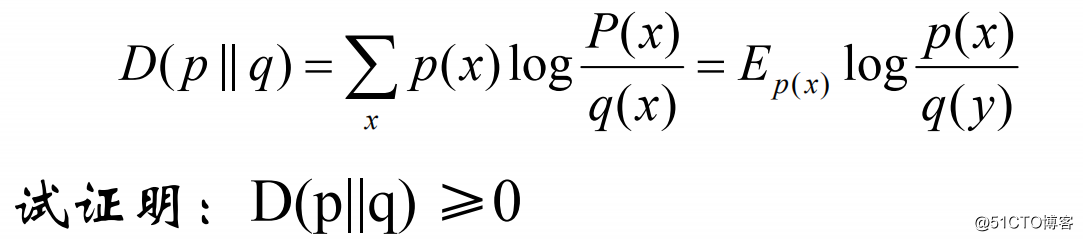
求解过程: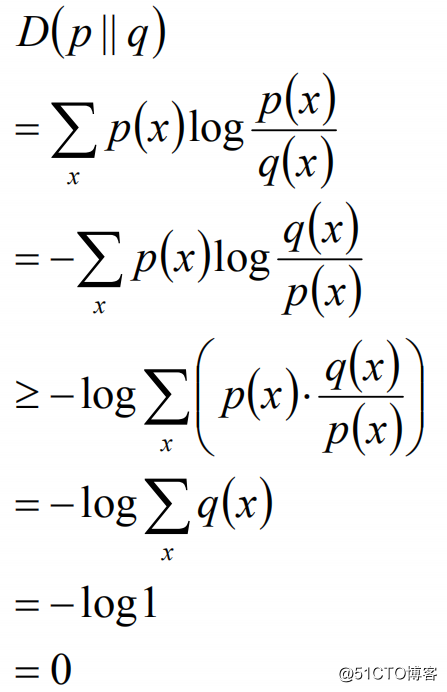
二、概率论:
1 古典概率例题:
举例:将n个不同的球放入N(N≥n)个盒子中,假设盒子容量无限,求事件A={每个盒子至多有1个球}的概率。
2装箱问题:
将12件正品和3件次品随机装在3个箱子中。每箱中恰有1件次品的概率是多少?
求解:
将15件产品装入3个箱子,每箱装5件,共有15!/(5!5!5!)种装法;
? 先把3件次品放入3个箱子,有3!种装法。对于这样的每一种装法,把其余12件产品装入3个箱子,每箱装4件,共有12!/(4!4!4!)种装法;
? P(A)= (3!*12!/(4!4!4!)) / (15!/(5!5!5!)) = 25/91
3 几个经典的概率公式:
4 各种分布模型
(1)0-1分布:
(2)二项分布:
(3)泊松分布:

(4)均匀分布: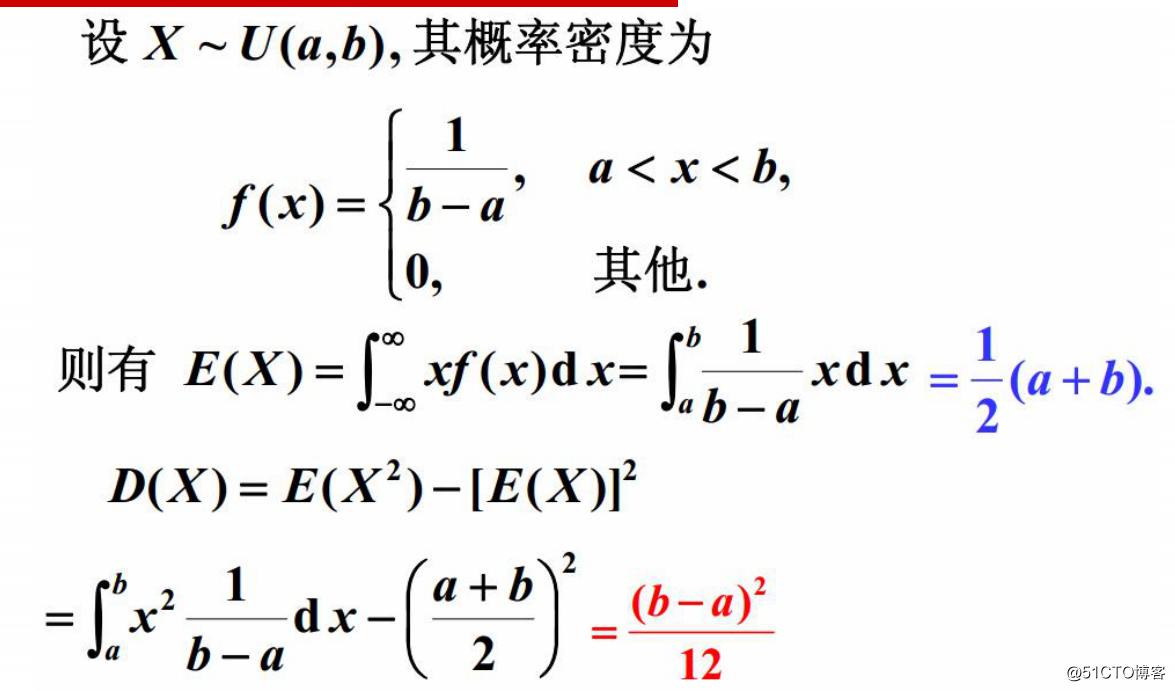
(5)指数分布:
(6)正态分布: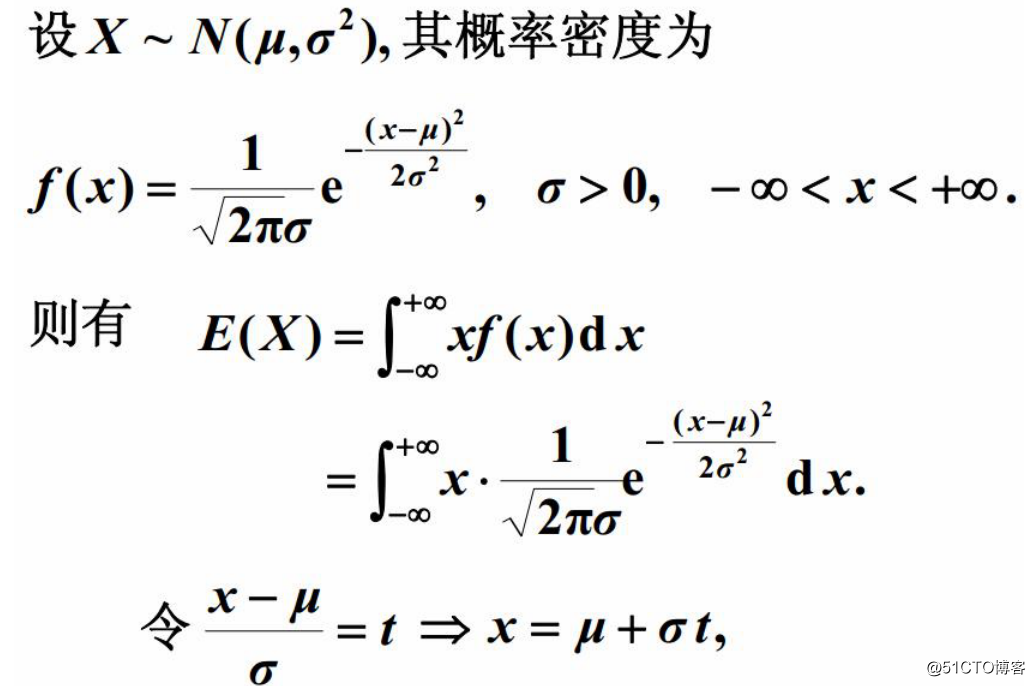
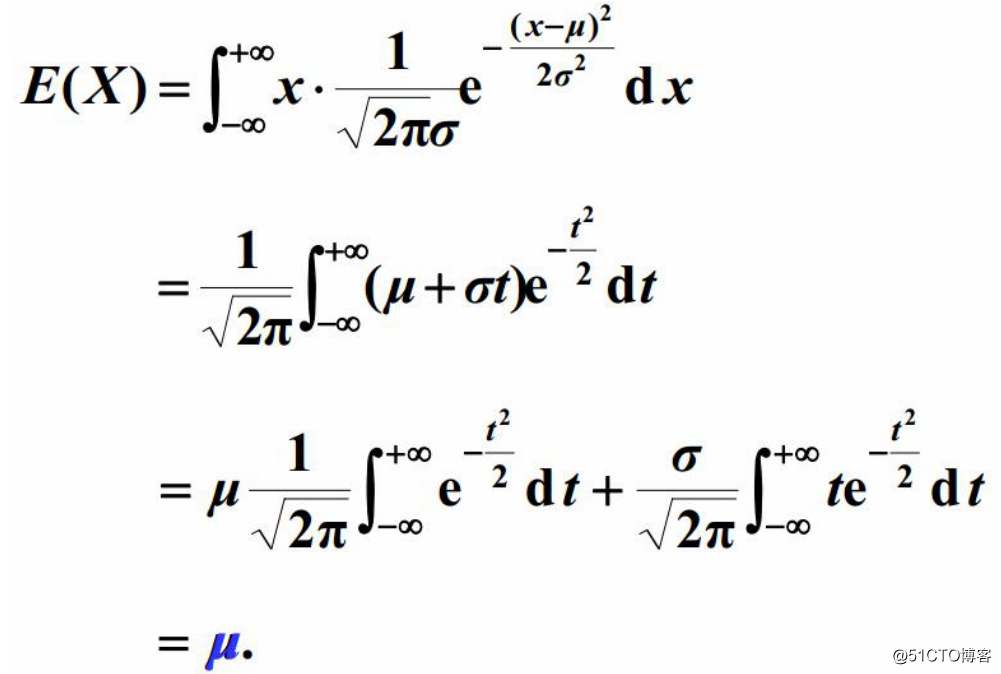
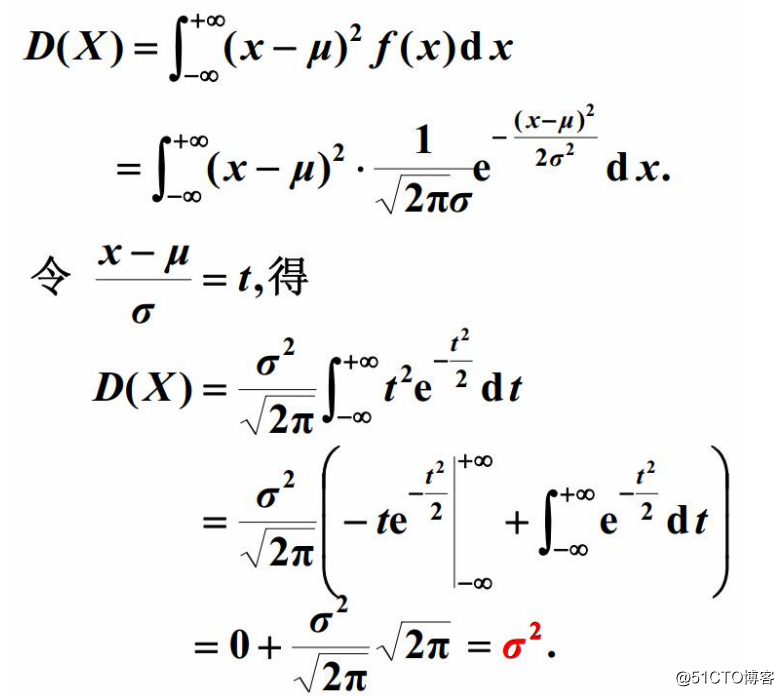
5 Logistic函数 :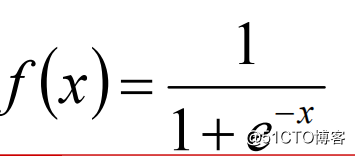
记住:f‘(x)=f(x)(1-f(x))
原文:http://blog.51cto.com/13831593/2173198