假设损失函数 loss = (w + 1)2。梯度是损失函数 loss 的导数为 ▽ = 2w + 2 。如参数初值为5,学习率为 0.2,则参数和损失函数更新如下:
1次 ·······参数w: 5 ·················5 - 0.2 * (2 * 5 + 2) = 2.6
2次 ·······参数w: 2.6 ··············2.6 - 0.2 * (2 * 2.6 + 2) = 1.16
3次 ·······参数w: 1.16 ············1.16 - 0.2 * (2 * 1.16 +2) = 0.296
4次 ·······参数w: 0.296
损失函数loss = (w + 1) 2 的图像为:
由图可知,损失函数 loss 的最小值会在(-1,0)处得到,此时损失函数的导数为 0,得到最终参数 w = -1。
代码 tf08learn 文件:https://xpwi.github.io/py/TensorFlow/tf08learn.py
# coding: utf-8
# 设损失函数loss = (w + 1)^2 , 令 w 是常数 5。反向传播就是求最小
# loss 对应的 w 值
import tensorflow as tf
# 定义待优化参数 w 初值赋予5
w = tf.Variable(tf.constant(5, dtype=tf.float32))
# 定义损失函数 loss
loss = tf.square(w + 1)
# 定义反向传播方法
train_step = tf.train.GradientDescentOptimizer(0.20).minimize(loss)
# 生成会话,训练40轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
for i in range(40):
sess.run(train_step)
W_val = sess.run(w)
loss_val = sess.run(loss)
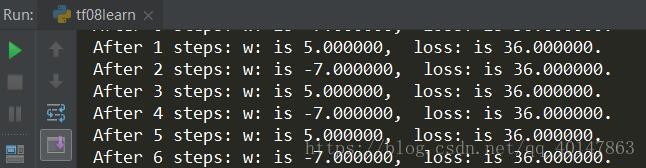
print("After %s steps: w: is %f, loss: is %f." %(i, W_val, loss_val))
运行结果分析: 由结果可知,随着损失函数值得减小,w 无线趋近于 -1

# coding: utf-8
'''
设损失函数loss = (w + 1)^2 , 令 w 初值是常数5,
反向传播就是求最优 w,即求最小 loss 对应的w值。
使用指数衰减的学习率,在迭代初期得到较高的下降速度,
可以在较小的训练轮数下取得更有收敛度
'''
import tensorflow as tf
LEARNING_RATE_BASE = 0.1 # 最初学习率
LEARNING_RATE_DECAY = 0.99 # 学习率衰减率
# 喂入多少轮 BATCH_SIZE 后,更新一次学习率,一般设置为:样本数/BATCH_SIZE
LEARNING_RATE_STEP = 1
# 运行了几轮 BATCH_SIZE 的计算器,初始值是0,设为不被训练
global_step = tf.Variable(0, trainable=False)
# 定义指数下降学习率
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step,
LEARNING_RATE_STEP, LEARNING_RATE_DECAY, staircase=True)
# 定义待优化参数 w 初值赋予5
w = tf.Variable(tf.constant(5, dtype=tf.float32))
# 定义损失函数 loss
loss = tf.square(w+1)
# 定义反向传播方法
# 学习率为:0.2
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
# 生成会话,训练40轮
with tf.Session() as sess:
init_op = tf.global_variables_initializer()
sess.run(init_op)
for i in range(40):
sess.run(train_step)
learning_rate_val = sess.run(learning_rate)
global_step_val = sess.run(global_step)
w_val = sess.run(w)
loss_val = sess.run(loss)
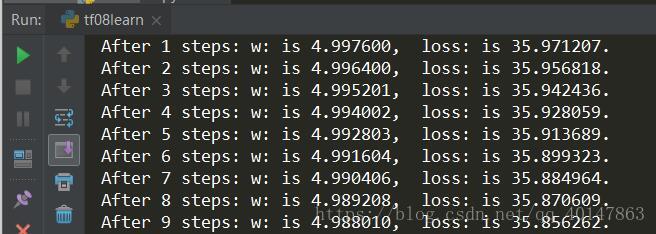
print("After %s steps: global_step is %f; : w: is %f;learn rate is %f; loss: is %f."
%(i,global_step_val, w_val, learning_rate_val, loss_val))
由结果可以看出,随着训练轮数增加学习率在不断减小
用 Tensorflow 函数表示:
**ema = tf.train.ExpoentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)
其中 MOVING_AVERAGE_DECAY 表示滑动平均衰减率,一般会赋予接近1的值,global_step 表示当前训练了多少轮
**ema_op = ema.apply(tf.trainable_varables())
其中 ema.apply() 函数实现对括号内参数的求滑动平均,tf.trainable_variables() 函数实现把所有待训练参数汇总为列表
with tf.control_dependencies([train_step, ema_op]):
train_op = tf.no_op(name=‘train‘)
(1)开始时,轮数 global_step 设置为 0,参数 w1 更新为 1,则滑动平均值为:
w1 滑动平均值 = min(0.99, 1/10)0+(1-min(0.99,1/10))1 = 0.9
(2)当轮数 global_step 设置为 0,参数 w1 更新为 10,以下代码 global_step 保持 100,每次执行滑动平均操作影子更新,则滑动平均值变为:
w1 滑动平均值 = min(0.99, 101/110)0.9+(1-min(0.99,101/110))10 = 0.826+0.818 = 1.644
(3)再次运行,参数 w1 更新为 1.644,则滑动平均值变为:
**w1
TensorFlow笔记-07-神经网络优化-学习率,滑动平均
原文:https://www.cnblogs.com/xpwi/p/9636391.html