D题 汽车总装线的配置问题
一.问题背景
某汽车公司生产多种型号的汽车,每种型号由品牌、配置、动力、驱动、颜色5种属性确定。品牌分为A1和A2两种,配置分为B1、B2、B3、B4、B5和B6六种,动力分为汽油和柴油2种,驱动分为两驱和四驱2种,颜色分为黑、白、蓝、黄、红、银、棕、灰、金9种。
公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小时)各230辆。每天生产各种型号车辆的具体数量根据市场需求和销售情况确定。附件给出了该企业2018年9月17日至9月23日一周的生产计划。
公司的装配流程如图1所示。待装配车辆按一定顺序排成一列,首先匀速通过总装线依次进行总装作业,随后按序分为C1、C2线进行喷涂作业。
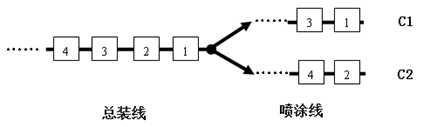
图1 汽车总装线的装配流程图
二.装配要求
由于工艺流程的制约和质量控制的需要以及降低成本的考虑,总装和喷涂作业对经过生产线车辆型号有多种要求:
(1)每天白班和晚班都是按照先A1后A2的品牌顺序,装配当天两种品牌各一半数量的汽车。如9月17日需装配的A1和A2的汽车分别为364和96辆,则该日每班首先装配182辆A1汽车,随后装配48辆A2汽车。
(2)四驱汽车连续装配数量不得超过2辆,两批四驱汽车之间间隔的两驱汽车的数量至少是10辆;柴油汽车连续装配数量不得超过2辆,两批柴油汽车之间间隔的汽油汽车的数量至少10辆。若间隔数量无法满足要求,仍希望间隔数量越多越好。间隔数量在5-9辆仍是可以接受的,但代价很高。
(3)同一品牌下相同配置车辆尽量连续,减少不同配置车辆之间的切换次数。
(4)对于颜色有如下要求:
1)蓝、黄、红三种颜色汽车的喷涂只能在C1线上进行,金色汽车的喷涂只能在C2线上进行,其他颜色汽车的喷涂可以在C1和C2任意一条喷涂线上进行。
2)除黑、白两种颜色外,在同一条喷涂线上,同种颜色的汽车应尽量连续喷涂作业。
3)喷涂线上不同颜色汽车之间的切换次数尽可能少,特别地,黑色汽车与其它颜色的汽车之间的切换代价很高。
4)不同颜色汽车在总装线上排列时的具体要求如下:
(a)黑色汽车连续排列的数量在50-70辆之间,两批黑色汽车在总装线上需间隔至少20辆。
(b)白色汽车可以连续排列,也可以与颜色为蓝或棕的汽车间隔排列;
(c)颜色为黄或红的汽车必须与颜色为银、灰、棕、金中的一种颜色的汽车间隔排列;
(d)蓝色汽车必须与白色汽车间隔排列;
(e)金色汽车要求与颜色为黄或红的汽车间隔排列;若无法满足要求,也可以与颜色为灰、棕、银中的一种颜色的汽车间隔排列;
(f)颜色为灰或银的汽车可以连续排列,也可以与颜色为黄、红、金中的一种颜色的汽车间隔排列;
(g)棕色汽车可以连续排列,也可以与颜色为黄、红、金、白中的一种颜色的汽车间隔排列。
(h)关于其他颜色的搭配,遵循“没有允许即为禁止”的原则。
由于该公司的生产线24小时不间断作业,以上总装线和喷涂线的各项要求对相邻班次(包括当日晚班与次日白班)的车辆同样适用。
三.需要解决的问题
(1)根据问题的背景、装配要求以及附件中的数据,建立数学模型或者设计算法,使其能给出符合要求、且具有较低生产成本的装配顺序。
(2)根据(1)中的数学模型或算法,针对附件中的数据,给出你们的计算结果:
(a)将9月20日的装配顺序按照下表格式填写在表中,并将此表放在论文的附录中。
首先这个题目描述的很多,中心思想就是调度,类似于公交车调度等问题,关键就是理清上面说的各种流程,然后入手,这个明显就是一个调度优化类问题,解决这类问题常见的算法就是规划模型,在这里很明显可以看出来是多目标规划,因为目标不唯一,当然我们也可以用智能算法的思想去优化,也可以基于运筹学方法。该方法主要针对传统的作业车间调度问题,在给定条件下,按某一衡量指标来寻找最优方案。它可以表示成求函数在满足约束条件下的极大极小值问题。常用的目标函数有拖期惩罚极小化、作业时间极小化等。运筹学方法具有适应性强,应用面广,计算技术比较简便的优点。但是由于运筹学方法自身的局限性,在运用运筹学方法时必须要附加一些脱离实际情况的假设,这在一定程度上使得其理论研究与实际应用之间存在差距。
启发式规则的定义为一个直观或经验的构造算法,在可以接受的花费(时间、空间)等条件下给出待解决组合优化问题的每个实例的一个可行解。启发式算法易于实现、计算复杂度低,在实际中得到了广泛的应用。可以将其分为简单规则、复合规则、启发式规则。启发式方法的缺点是不一定能保证得到的解的可行性和最优性,甚至在多数情况下,无法阐述所得解同最优解的近似程度。也可以选用自适应神经网络和启发式算法混合方法进行调度,我们直接讲算法通过MATLAB编程带入进去就行了。
原文:https://www.cnblogs.com/ECJTUACM-873284962/p/9663349.html