题目链接:https://nanti.jisuanke.com/t/31716
题目大意:有n个孩子和n个糖果,现在让n个孩子排成一列,一个一个发糖果,每个孩子随机挑选x个糖果给他,x>=1,直到无糖果剩余为止。给出数字n,问有多少种分发糖果的方法。
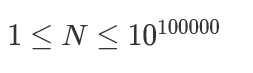
1
4
8
解题思路:我们可以这样想,一个糖果的话,应该是只有1种方法记为x1,如果是两个糖果的话,有两种方法即为x2,分别为(1,1)和(2),从中我们可以想到如果n个糖果的话,就可以分为第n个人取1个的话就有x(n-1)种,去两个的话就有x(n-2)种,依次类推,第n个人取n-1个的话就有x1种方法,第n个人取n个的话就只有1种方法。即x(n)=x1+x2+……+x(n-1)+1=2^(n-1);
其实就是一个简单的拆数问题,比如这里有三个学生,老师有三个糖果,有四种分法:{3,0,0},
{2,1,0},{1,2,0},{1,1,1}
一个数的拆法其实就是2^(N-1)
也可以打表找规律,都很简单。
但是有一个难点是n的范围特别大,可以达到10^100000,不能通过整型数字存储,而只能用字符数组存储这个数,这样的话我们肯定不能直接用快速幂。所以这里就要采用一个小技巧,也就是一个性质,2^N模一个质数,它的结果是具有周期性的,周期长度为mod-1,这道题就利用这个周期
性质,具体步骤就是:先把n转化成模mod-1下的的数,然后用这个数计算快速幂。
附上代码:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
char s[100005];
ll qpow(ll a,ll n)
{
ll ans=1;
while(n)
{
if(n&1) ans=(ans*a)%mod;
n>>=1;
a=(a*a)%mod;
}
return ans;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
scanf("%s",s);
int len=strlen(s);
ll MOD=mod-1,temp=0;
for(int i=0;i<len;i++)
temp=(temp*10+s[i]-‘0‘)%MOD; //将n转化成mod-1内的数
if(temp==0) temp=MOD; //特判temp==0时,temp即为mod-1
temp=(temp-1+MOD)%MOD;
ll ans=qpow(2,temp);
cout<<ans<<endl;
}
return 0;
}
ACM-ICPC 2018 焦作赛区网络预赛 G. Give Candies (打表找规律+快速幂)
原文:https://www.cnblogs.com/zjl192628928/p/9678184.html