题目描述
有一楼梯共m级,刚开始时你在第一级,若每次只能跨上一级或二级,要走上第m级,共有多少走法?
注:规定从一级到一级有0种走法。
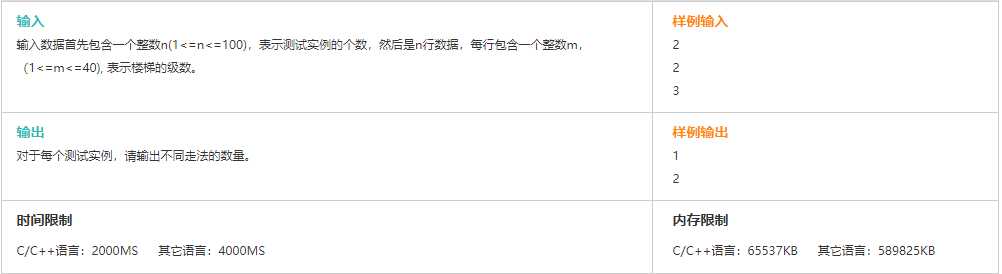
分析:
1.从第一阶到第N阶,需上n=N-1个台阶
2.每次可上1~2个台阶,即可转化问题为n有几种由1和2组成的方法
3.n最少由n%2个1和floor(n/2)个2组成,每个2可转化为2个1(设floor(n/2)+n%2=M,n%2=K)
4.1和2的排列组合应当是M!/[K!*(M-K)!];即在M个数中,以1为定位的排列组合数
代码:
1 <?php 2 $handle=fopen(‘php://stdin‘,‘r‘); 3 $n=trim(fgets($handle)); 4 for($i=0;$i<$n;$i++){ 5 $num=trim(fgets($handle)); 6 print(getNum($num-1)."\n"); 7 } 8 9 function getNum($num){ 10 $sum=0; 11 $one=$num%2; 12 $n=(int)($num/2); 13 14 15 for($j=$one;$j<=$num;$j+=2){ 16 $sum+=product($n+$j,$j); 17 $n--; 18 } 19 return $sum; 20 } 21 22 function product($n,$k){ 23 return $num=jieC($n)/(jieC($n-$k)*jieC($k)); 24 } 25 26 function jieC($n){ 27 if($n==1||$n==0){ 28 return 1; 29 } 30 return $n*jieC($n-1); 31 }
遇错:
1.#line12 取2的个数:$num/2 时,初始并没有在意数据类型,遇错后使用了round()函数【格式化数字,四舍五入】,结果自然不对,然后又用了ceil()函数【进一取整】自然又不对,使用了强制转换(int)正确,后又查了舍去小数部分取整的函数是floor();
2.#line27 在做递归求阶乘时开始没有考虑输入0的情况,结果自然是。。
另解:
提交之后发现好多人的解法并不是这样,而是这样
java:
1 import java.util.Scanner; 2 3 public class Main { 4 public static void main(String[] args) { 5 Scanner sc = new Scanner(System.in); 6 7 while(sc.hasNext()) { 8 int num = sc.nextInt(); 9 for(int i=0; i<num; i++) { 10 System.out.println(Fan(sc.nextInt())); 11 } 12 } 13 14 } 15 public static int Fan(int n) { 16 if(n == 1) return 0; 17 if(n == 2) return 1; 18 if(n == 3) return 2; 19 return Fan(n-1)+Fan(n-2); 20 } 21 }
php:
1 <?php 2 fscanf(STDIN,"%d",$n); 3 for($i=0;$i<$n;$i++){ 4 fscanf(STDIN,"%d",$m); 5 if($m == 1) 6 echo 0,PHP_EOL; 7 else if($m == 2) 8 echo 1,PHP_EOL; 9 else if($m == 3) 10 echo 2,PHP_EOL; 11 else{ 12 $f2=1;$f3=2;$res=0; 13 for($j=4;$j<=$m;$j++){ 14 $res = $f2+$f3; 15 $f2 = $f3; 16 $f3 = $res; 17 } 18 echo $res,PHP_EOL; 19 } 20 }
注:本来我以为在赛码网不能用 fscanf(STDIN,"%d",$n);每次都需要写老长的fopen,这回开窍了,在本地测试时加了
1 <?php 2 define(‘STDIN‘,fopen(‘stdin‘,‘r‘)); 3 ?> 4 <?php 5 fscanf(STDIN, "%d %d %d", $x,$y,$s);
##感觉自己是个智障
这个方法是斐波那契数列,然而我是不知道怎么得到这个的。。。难道是列举之后发现的?有大佬知道请告诉我。
原题:http://exercise.acmcoder.com/online/online_judge_ques?ques_id=1668&konwledgeId=134
原文:https://www.cnblogs.com/mudaoyuye/p/9716139.html