毒瘤最优化(min)
【题目背景】
NOIP2018 即将到来,一个新的轮回就要开始。
新时代的 BSOIer:加油,未来是 你们的!
【题目描述】
定义一棵树 T 的生成毒瘤图 G 为拥有和 T 同样个数的节点,且任意两点之间都 存在带权边,其边权等于树上那两点的带权距离。
定义一棵树的毒瘤值为其生成毒瘤图上的最长曼哈顿回路。
作为一名良心的出题人,苣蒻 AChen 不喜欢过于毒瘤的树,因此找来你给树上每 条边赋上边权,要求边权必须为互不相同的正整数,且最小化这棵树的毒瘤值,请你输 出这个值。
(数据保证最优解不超过 64 位整形范围)
【输入格式】
从文件 min.in 中读入数据。
输入的第一行包含一个正整数 n,保证 n ≤ 1000000,表示树的节点总数。
第二行至第 n 行,每行两个整数 u, v,表示树的一条边。
【输出格式】
输出到文件 min.out 中。
输出一个整数,表示最小的毒瘤值。
【样例 1 输入】
2
1 2
【样例 1 输出】
2
【样例 1 解释】
由于只有一条边,最小的毒瘤值显然是 2。
【样例 2】
见选手目录下的 min/min2.in 与 min/min2.ans。
【子任务】
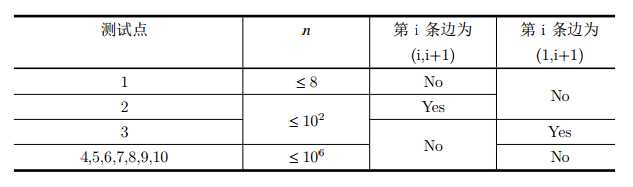
【提示】
数据保证最优解不超过 64 位整形范围。
今天T1之前做过不放了
这题我实在是个SB。。。。。被他的哈密顿回路给搞成以为是完全图,然后我就floyd+状压压过去,现在想想想打自己!!
首先我们先看子任务的链状结构,不难得出最长的路径肯定是左一个右一个。
那么我们再次递推一下规律
考虑我们选择遍历的点的顺序是x1,x2.....对于他们一共的距离实际上就是
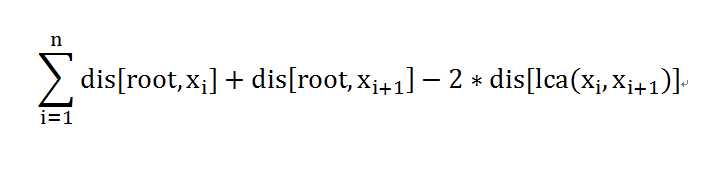
所以实质上就是我们要让lca距离最短就是最长
考虑以树的重心为根,一定存在一种方案使每一对点的lca都是根(证明略)
所以对于每一条边(x,fa[x])会经历2*siz[x]次,统计排序就完了
这道题简直要吐血了,把一棵树当图来做,我是不是该现在退役了。。。。
code:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define N 2100005 6 using namespace std; 7 struct node{ 8 int u,v; 9 }e[N]; 10 int n,mark=9999999,root,first[N],nxt[N],cnt,siz[N],h[N],tot; 11 void add(int u,int v){ 12 e[++cnt].u=u; 13 e[cnt].v=v; 14 nxt[cnt]=first[u]; 15 first[u]=cnt; 16 } 17 void dfs1(int x,int father){//树的重心 18 siz[x]=1; 19 int max0=0; 20 for(int i=first[x];i;i=nxt[i]){ 21 int v=e[i].v; 22 if(v==father)continue; 23 dfs1(v,x); 24 siz[x]+=siz[v]; 25 } 26 if(x!=1) 27 h[++tot]=2*min(siz[x],n-siz[x]); 28 } 29 void read(int &x)//‘&‘表示引用,也就是说x是一个实参,在函数中改变了x的值就意味着在外面x的值也会被改变 30 { 31 int f=1;//标记正负 32 x=0;//归零(这就是潜在bug,有可能传进来时x没有归零) 33 char s=getchar();//读入第一个字符 34 while(s<‘0‘||s>‘9‘)//不是数字字符 35 { 36 if(s==‘-‘)//不能直接把f=-1,有可能输入的不是‘-‘而是其他乱七八糟的东西 37 f=-1; 38 s=getchar();//继续读 39 } 40 while(s>=‘0‘&&s<=‘9‘)//是字符(一旦不是字符就意味着输入结束了) 41 { 42 x=x*10+s-‘0‘; 43 s=getchar(); 44 } 45 x*=f;//改变正负 46 } 47 int main(){ 48 freopen("min.in","r",stdin); 49 freopen("min.out","w",stdout); 50 cin>>n; 51 for(int i=1;i<n;i++){ 52 int a,b; 53 read(a),read(b); 54 add(a,b); 55 add(b,a); 56 } 57 dfs1(1,0); 58 sort(h+1,h+tot+1); 59 int now=1; 60 long long ans=0; 61 for(int i=1;i<=tot;i++) 62 ans+=h[i]*(tot-i+1); 63 cout<<ans; 64 return 0; 65 }
over
原文:https://www.cnblogs.com/saionjisekai/p/9724273.html