[NOIP2018校模拟赛]T2矩阵分组 Matrix

题目链接：

矩阵分组

分析：

这道题求的是两部分极差当中大的那个的最小值。对于这种求最值的问题，我们很自然（其实并没有）地想到二分答案。

这个题有两个结论：
（好像当时看出来了第一个？然后发现下面都不会了，果断弃疗滚去写T3）

第一个结论：

对于划分的每个区域，为了保证只拐一次弯，它每一行的长度是单调且连续的

这样任意两个元素之间拐个直角弯就能到了（x）

参见下图（从发的solution里面扒的）：

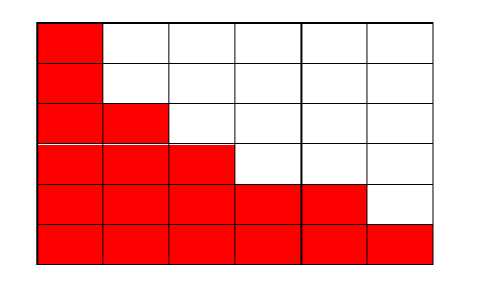
这个结论可以感性得到（……），因为如果它每一行的长度不单调，就会有 凸 ←这种形状的东西出来，从它的一边到另外一边肯定是要拐至少两个弯的

第二个结论：

矩阵A和矩阵B可以互换（即它们是等价的）

因为每个矩阵不管怎么讲总要占据一个角落（否则不满足结论1），所以先考虑A占据左上角的情况，然后把它旋转三次就能涵盖到所有情况。
二分一个值mid（mid=min(max(gmaxi1-gmini1,gmaxi2,gmini2)），其上界为矩阵中最大值-最小值，下界为0，这样最后的mid就是答案

对于check函数的思路：

因为矩阵中最大值和最小值不能在一个区域，否则这个max(gmaxi1-gmini1,gmaxi2,gmini2)就会很大，所以我们不妨设tot_max在A区域
从第一行开始找到第一个（找第一个是为了保证单调）与tot_max差值大于mid的值，这时候就跳出循环（这里每一行的枚举不能超过上一行的边界），后面同理，处理出矩阵A，显然这个矩阵A一定是满足条件的
然后我们验证剩下的部分（即矩阵B）当中的极差是否小于等于mid即可

代码：

没有代码，因为我还没写出来（……）

#include<bits/stdc++.h>
using namespace std;
int n,m,x=1,x1=1,x2=n,x3=m,y=1,yy=n,y2=m,y3=1,t;
int tot_max=-(1<<20),tot_min=1<<20;
int a[4][2005][2005],endi[2005];  //endi中存储A矩阵每行的边界 
inline int read(){
    int cnt=0,f=1;char c;
    c=getchar();
    while(!isdigit(c)){
        if(c==‘-‘)f=-1;
        c=getchar();
    }
    while(isdigit(c)){
        cnt=cnt*10+c-‘0‘;
        c=getchar();
    }
    return cnt*f;
}
bool check(int kind,int x){
    if(kind&1) swap(n,m);  // 这里第二和第四个矩阵是分别顺时针逆时针旋转了90°的，所以行数和列数需要交换 
    endi[0]=m;
    int tag;
    for(register int i=1,j;i<=n;i++){
        for(j=1;j<=endi[i-1];j++){
            if(tot_max-a[kind][i][j]>x)  //找到第一个与tot_max差值小于等于mid的值 
                break;
            }
            endi[i]=j-1;
        }
    for(register int i=1;i<=n;i++)
        for(register int j=endi[i]+1;j<=m;j++)  //处理第二个矩阵
            if(a[kind][i][j]-tot_min>x){
                if(kind&1) swap(n,m);  //如果刚刚交换了n和m，为了下次check，这里需要换回来 
                return false;
            }
    if(kind&1) swap(n,m);
    return true;
}
bool tot_check(int x){
    if(check(0,x))return true;
    if(check(1,x))return true;
    if(check(2,x))return true;
    if(check(3,x))return true;
    return false;
}
int main(){
    n=read();m=read();
    x=1,x1=1,x2=n,x3=m,y=1,yy=n,y2=m,y3=1;
    for(register int i=1;i<=n;i++){  //读入矩阵，读入的时候就可以顺手旋转成四个矩阵了（顺便这个旋转很巧妙啊） 
        for(register int j=1;j<=m;j++){
            t=a[0][x][y++]=a[1][x1++][yy]=a[2][x2][y2--]=a[3][x3--][y3]=read();
            if(t>tot_max)tot_max=t;
            if(t<tot_min)tot_min=t;
        }
    x++,y=1,yy--,x1=1,x2--,y2=m,y3++,x3=m;
    }

    int l=0,r=tot_max-tot_min;
    int mid=(l+r)>>1;
    while(l<r){
        if(tot_check(mid)){
            r=mid;
            mid=(l+r)>>1;
        }
        else{
            l=mid+1;
            mid=(l+r)>>1;
        }
    }
    printf("%d",mid);
    return 0;
}

[NOIP2018校模拟赛]T2矩阵分组 Matrix

原文：https://www.cnblogs.com/kma093/p/9739035.html