Dirichlet分布
我们把Beta分布推广到高维的场景,就是Dirichlet分布。Dirichlet分布定义如下
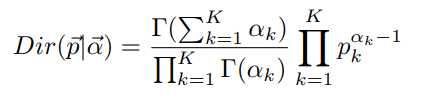
Dirichlet分布与多项式分布共轭。多项式分布定义如下
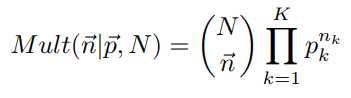
共轭关系表示如下
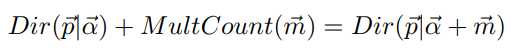
Dirichlet-MultCount共轭理解
上述共轭关系我们可以这样理解,先验Dirichlet分布参数为α,多项式分布实验结果为m,则后验Dirichlet分布的参数为α+m。m为n维向量,表示实验中各种结果出现的次数。例如投掷骰子的试验中,m为6维向量,6个分量分别表示出现1点到6点的次数。
一般来说,我们使用贝叶斯定理推断Dirichlet-MultCount共轭关系。对于参数为α的Dirichlet分布,可以用如下公式表示
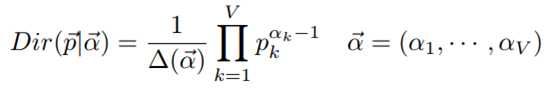
这里,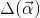 表达式如下
表达式如下
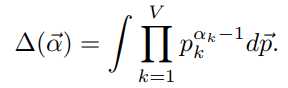
进行了多项式分布实验后,得到结果n后,后验分布为
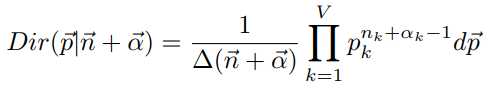
参数n与α确定后,后验分布的期望为
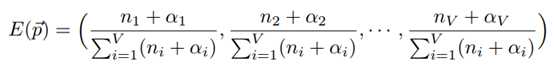
原文:https://www.cnblogs.com/coshaho/p/9740168.html