建立方程

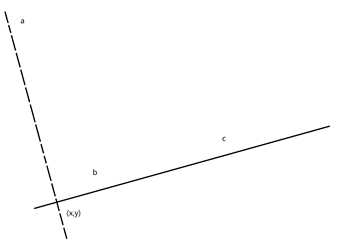
设a为直线外一点，b,c为直线上两点

$\left\{ \begin{matrix}

(x-ax,y-ay)\cdot (cx-bx,cy-by)=0 \

\frac{y-cy}{x-cx}=\frac{y-by}{x-bx} \

\end{matrix} \right.$

?

解出符号解

使用mathematics工具：

1. Solve[{(x?-?ax)*(cx?-?bx)?+?(y?-?ay)*(cy?-?by)?==???
2. ???0,?(y?-?cy)*(x?-?bx)?==?(y?-?by)*(x?-?cx)},?{x,?y}]??

得出如下：

1. {{x?->?-(((bx?-?cx)?(ax?bx?+?ay?by?-?ax?cx?-?ay?cy)?-?(-by?+???
2. ????????cy)?(by?cx?-?bx?cy))/((bx?-?cx)?(-bx?+?cx)?-?(-by?+?cy)^2)),???
3. ??y?->?-((-ax?bx?by?-?ay?by^2?+?ax?by?cx?+?bx?by?cx?-?by?cx^2?+???
4. ????????ax?bx?cy?-?bx^2?cy?+?2?ay?by?cy?-?ax?cx?cy?+?bx?cx?cy?-???
5. ????????ay?cy^2)/(bx^2?+?by^2?-?2?bx?cx?+?cx^2?-?2?by?cy?+?cy^2))}}??

然后可以将上式带入需要的程序中，求得垂足。

二维平面上向量与向量外一点的垂足符号解

原文：https://www.cnblogs.com/didea/p/9745087.html