Ahead

10.5.2018

First

计算几何的入门，凸包问题做引子。

凸包??（定义）

百度百科的定义：（不重要）
在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1，...Xn)的凸组合来构造.
在二维欧几里得空间中，凸包可想象为一条刚好包著所有点的橡皮圈。
用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中所有的点。
下图就是一个凸包，不过概念大概理解一下就可以了

Attention！

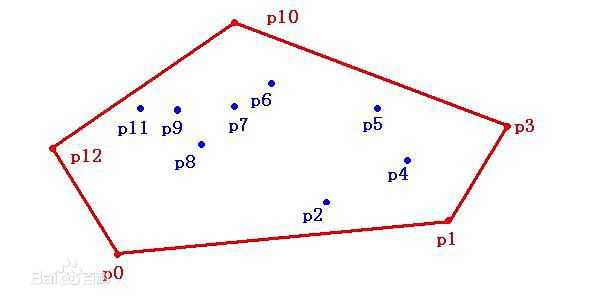
当点变化时，凸包上的极点（定义后面加，就是线上的点）可能增加可能减少

【学习笔记：CG基础1】 Convex Hull

原文：https://www.cnblogs.com/PiCaHor/p/9745919.html