可能这是我的巅峰了吧.

这题什么意思呢.
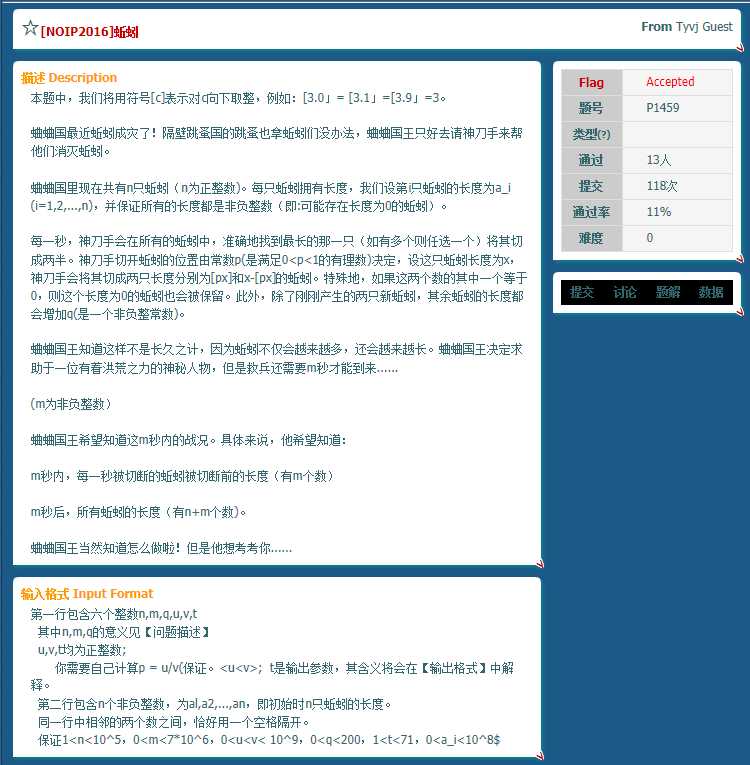
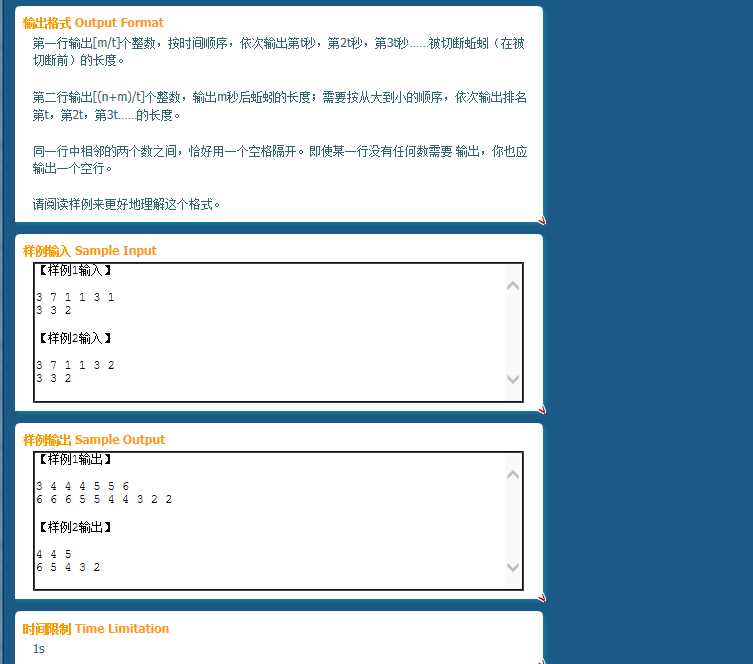
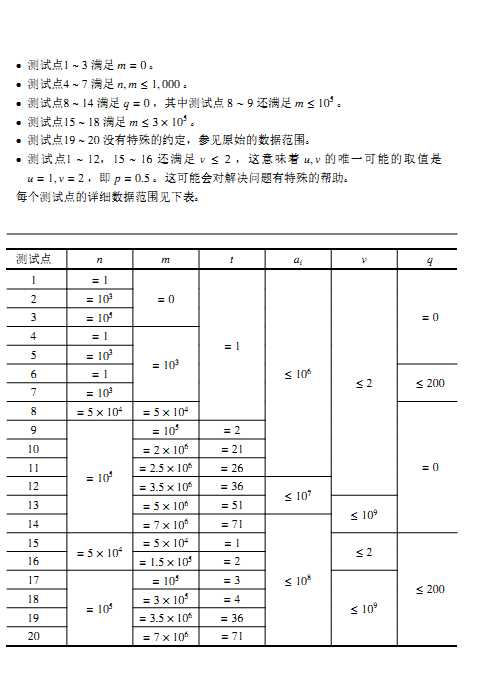
有一堆数,m秒内总选取最大的一个下手:把它分成?x*u/v?和x-?x*u/v?.其他的都增长q;求每秒内的最大数和最后的所有剩下的数.
(本题可以上一个优先队列很快的就水了,但是oj不允许哇.)
考虑不增长的时候怎么做?我们来开三个队列.先把最开始的长度排序后放入第一个队列里,找到三个队头的最大值分一下后就分别扔到两个队列里.然后再找最大值...
考虑为什么这样做是正确的.
这是因为两个队列是历史上最大值分下来的,只要你放的顺序不变,先进入的一定是更大值分得的,比后进入的大.这样子三个队列内部都是递减的,而且二三个队列总大于新的最大值分到的.
输出的时候就还是不断的对三个队列找最大值后输出.
考虑增长的时候怎么做.
可以利用差分的思想,或者说利用时间戳?我们记录每一个数分的时候的时间,也就是刚开始全部为1,23队列是循环的时候的i值.这样求值的时候只需把队列中的值加上q*(i-t)就好.然后分了之后重新记时间.
输出的时候同理.
就很开心的写了一个重载运算符.代码瞬间简介(
//全代码不敢用.size() int i,t; int n,m,q,T; double u,v; int now,e1,e2,e3; struct aba:queue<int> { }; int operator + (const aba &a,const aba &t) { if(a.empty())//如果为空 return -1000000;//交的时候没这么小,还好没卡我 return a.front()+q*(i-t.front());//这是为什么下面输出的时候让i=m+1而让一个n控制循环的原因 } aba a1; aba a2; aba a3; aba t1; aba t2; aba t3; aba ans; inline int maxx() { e1=a1+t1;e2=a2+t2;e3=a3+t3; if(e1>=e2&&e1>=e3) { a1.pop();t1.pop(); return e1; } if(e2>=e1&&e2>=e3) { a2.pop(); t2.pop(); return e2; } a3.pop();t3.pop(); return e3; } int o[1000000]; inline bool Orz(int a,int b) { return a>b; } int main() { n=read(),m=read(),q=read(),u=read(),v=read(),T=read(); for(i=1;i<=n;i++) o[i]=read(); sort(o+1,o+1+n,Orz); for(i=1;i<=n;i++){ a1.push(o[i]); t1.push(1); } for(i=1;i<=m;i++){ now=maxx(); if(i%T==0) cout<<now<<‘ ‘; a2.push(int(now*u/v)-q); t2.push(i); a3.push(now-int(now*u/v)-q);//注意取整的位置 t3.push(i); } cout<<endl; i=m+1; for(n=1;!a1.empty()|| !a2.empty()|| !a3.empty();n++){ now=maxx(); if(n%T==0) cout<<now<<‘ ‘; } }
原文:https://www.cnblogs.com/qywyt/p/9746532.html