想了很久。。首先本渣渣就不太理解递归在python中的实现,其次又不知道怎么去找到最长路径,真是很费脑子,开始正题吧
首先明确二叉树每个节点都可以看作“根节点”,依次延伸下去(二叉树的递归定义),对于根节点,我要求这个节点的最大深度,那么只要求两棵左右子树的最大深度,并且max一下,然后+1就行了;然后对于左右两棵子树,也只要求它们的两棵左右子树的最大深度,然后max一下并且+1就行了。。。。。到了叶子节点,它没有左右两棵子树了,那么它的最大深度就直接赋值为1,然后一层一层往上去实现(刚才是往下展开),就可以求出根节点到最底层叶子节点的最大深度,简直是很牛逼的思路!
给出代码具体分析:
class Solution: def TreeDepth(self, pRoot): # write code here if pRoot == None: return 0 lDepth = self.TreeDepth(pRoot.left) rDepth = self.TreeDepth(pRoot.right) return max(lDepth,rDepth)+1
假设有如下二叉树,
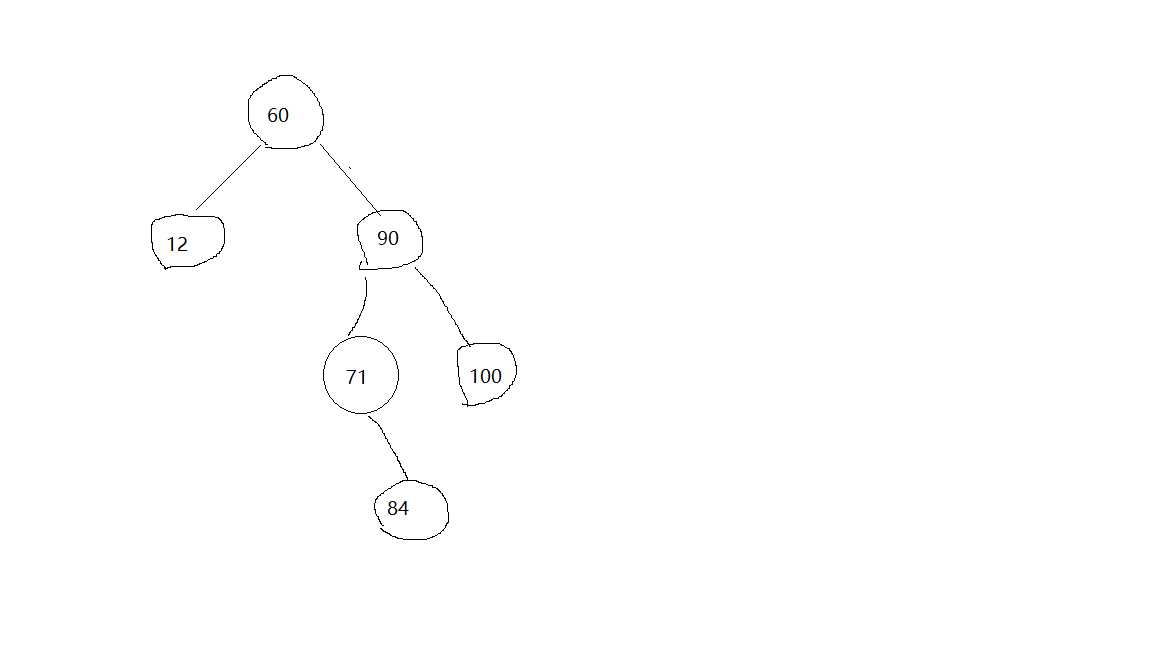
代码执行情况如下:
首先十分明确的一点是,TreeDepth(60)的结果就是返回值,就是要求出来的,不要被递归函数的压栈、出栈给混淆了,return的一定是TreeDepth(根节点)的返回值
TreeDepth(60)= max(TreeDepth(12),TreeDepth(90))+1,OK,求那两个未知的值
TreeDepth(12)是1,因为它的左右节点都不存在,两个返回值都是0,所以max()+1之后就是1,
而TreeDepth(90)这个东西,也要一层层递归下去求解,容易看出来,这个值是3
最后,max(TreeDepth(12),TreeDepth(90))+1求出来就是4
原文:https://www.cnblogs.com/yqpy/p/9748963.html