逻辑回归用于分类问题。
对于二分类问题,输入多个特征,输出为是或不是(也可以写作1或0)。
逻辑回归就是这样一个用于分类的模型。
逻辑回归建立在线性回归的基础上。
首先,线性回归将多个特征映射到一个变量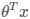 。
。
之后,在这个变量上设置一个阈值。大于这个阈值的判断为是,输出1;小于这个阈值的判断为否,输出0。
也可以不输出1或0,而输出是1的概率,再由概率是否大于0.5判断是或否。
逻辑回归就是这样一个输出是1的概率的模型(Sigmoid函数):
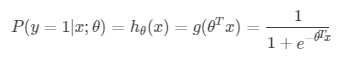
对于θTx,判断输出是否为1的阈值为θTx=0。
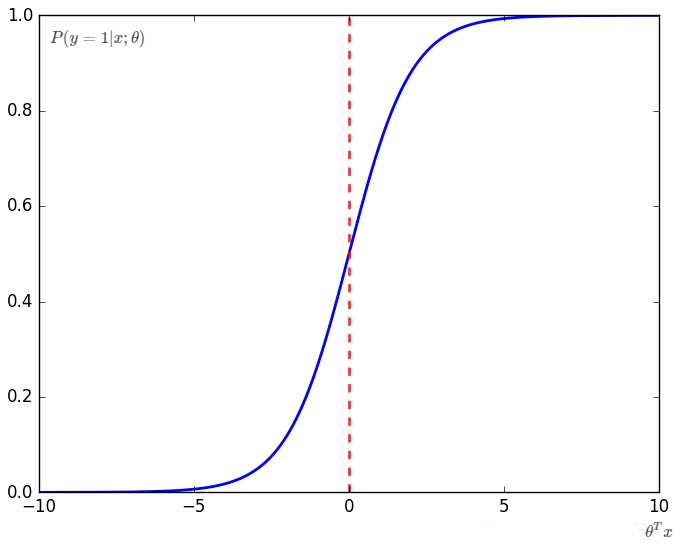
假设我们找到了一个合适的逻辑回归模型,那么,等价于确定了一组θ,使θTx=0是合适的阈值。此时,θTx=0将特征空间分割开了,就叫做Decision Boundary。
实际上,Decision Boundary就是对训练后的模型的另一种描述。
为了评估模型拟合的程度,类比于线性回归,也需要Cost Function,线性回归的Cost Function不适用于逻辑回归。
需要寻找一种判断偏差的方法。
对于单个样本,考察一下对数函数:
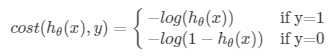
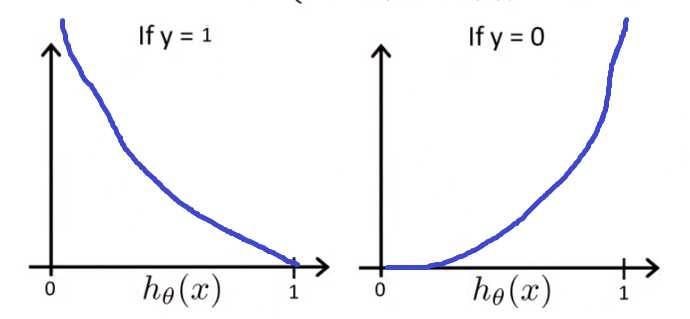
当实际是1时,是1的概率越大(h代表概率),偏差越小。同样,当实际是0时,是1的概率越大,偏差越大。
所有样本的偏差求和,Cost Function可以写作下式
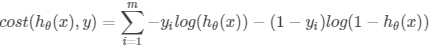
最简单的还是梯度下降。公式再写一次:
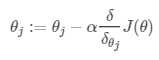
详细推导及求偏导数可见:详解。
此外,还可以用conjugate gradient、BFGS、L-BFGS等算法计算参数,效率更高,但比较复杂,不容易调试。
对于封装好的算法,只需要提供Cost Function和偏导数,可以自动选择α和计算了。
%data.csv [feature1 feature2 y]
sample = csvread(‘data.csv‘);
x(:,2) = sample(:,1);
x(:,3) = sample(:,2);
y(:,1) = sample(:,3);
x(:,1) = ones(size(x(:,2)));
m = length(x(:,2));
%choose logistic regression as model
%start with
theta = [1;2;1];
alpha = 1;
times = 5000;%迭代次数
J_theta = [1:times];
%cost function J_theta & gridient gri_J using gridient descent
for i=1:times
H = 1./(1+exp(-x*theta));
J_theta(i) = (-1/m) * (log(H‘)*y+log(1-H‘)*(1-y));
gri_J = (1/m).*((H-y)‘ * x)‘;
theta = theta - alpha.* gri_J;
end
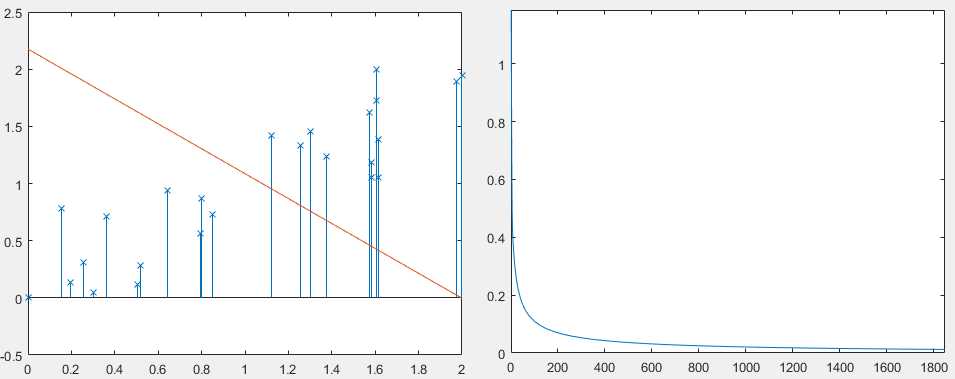
plot(J_theta);
% deci_bond_y = -(1/theta(3)).*(theta(1)+theta(2).* x(:,2));
%
% stem(x(:,2),x(:,3),‘x‘);
% hold on;
% plot(x(:,2),deci_bond_y);
对于每个类别,看做这个类别和“”其他类别“”(课程里叫one versus all),这样就变回二元分类了。
再对每种类别分别做二元分类,得到N个分类器。
当需要测试时,将数据输入到每个分类器,选概率最大的一个作为输出。
逻辑回归建立在线性回归的基础之上。模型为:通过sigmoid函数求输出是1的概率。应用在输出应符合伯努利分布的情况。
梯度下降算法还是好用的,也有了一些更高效的算法。刚开始的时候,可以先拿来用,再慢慢去深入学习。
线性回归和逻辑回归用于处理不同问题,但使用方法都是:分析数据、选取模型、优化数据、选择算法、训练、得到训练后的模型。
原文:https://www.cnblogs.com/sumr/p/9750145.html