Ahead

10.7.2018

定义

三角剖分：

1. 将一个多边形分为几个不重叠的三角形
   2.对点集的三角剖分
   
   对角线：连接多边形非相邻的顶点一条线段。
   内对角线：没有穿过多边形边界的对角线
   对偶图：对于原图中的每一个面化为一个点，如果两个面之间有线，那么在两个点引出一条线，新构即为对偶图
   

   Art Gallery Problem

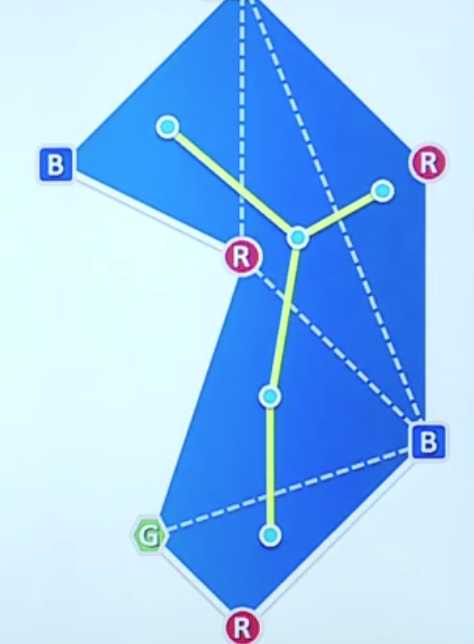
   描述：在一个多边形中至少需要几个点（每个点能够无限放射）将其覆盖。
   特例：正多边形，显然只用一个，与此同时凸包也是这样的，星行多边形同样也是如此。
   最差的情况：n个，1-1顶点。 （仅限于二维）
   这是一个NP-hard问题
   简化问题如果只能在顶点上
   然而
   这是一个NP-hard问题
   再次简化
   如果这个点可以在边上移动
   然而
   这是一个NP-hard问题
   再次简化，如果所有的边都是垂直的还是水平的
   然而
   这是一个NP-hard问题
   那么我们尝试覆盖上面的特例的一般性情况
   结论 最多n/3足以
   
   即内一个尖端都需要一个
   而这个的证明，正是从三角剖分出发的（Fisk Proof）
   所以你可以忽略上面的

   性质

   三角剖分的对偶图一定是一颗树
   结论：对于一个三角剖分图染色，至多只用三种颜色，使得相连边两端颜色不同 （三角剖分的三染色）
   那么染色问题就可以转换为覆盖问题，只用染其中同色点（最小集）就能覆盖整个Polygon

   变种：Orthogonal Polygons

   正交多边形（所有边水平或垂直）
   结论：对于OP 它最多只需n/4个点
   证明将形成凸四边形剖分。 同上的一系列结论 （四染色问题）

   正题：三角剖分

• 界定： 三角剖分一定存在仅当为Simply Polygons （也成Jordan Polygons）（边不交，顶点不重合）时

  空洞？ 存在 （边界切割先）

• 整理一下就是只要是SP 无论是否有空洞，一定存在三角剖分

  Proof and Algorithm （Ear-Cutting）

  定义：Ear： 如果一个点和它的前驱后继构成的点完全落在Polygon内，那么这个局部就是Ear ，而该点为 a tio of the ear
  
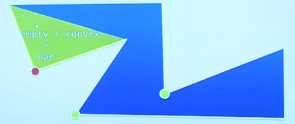
  （黄部）
  Mouth：相反的，如果一个点和它的前驱和后继构成的三角形完全落在外面，那么这就是一个mouth。
  
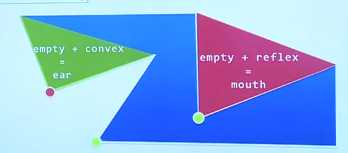
  （红部）
  Dirty： 介于两者之间的状况
  
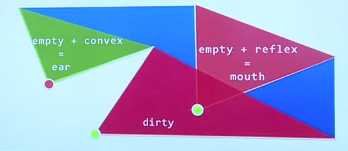
  （深红部）

【学习笔记：计算几何基础5】 Triangulation

原文：https://www.cnblogs.com/PiCaHor/p/9751000.html