线段树（SegmentTree）学习笔记

在对数组进行操作的时候，我们有时会需要获取数组某个区间的信息，如该区间内的最值、区间和等。我们可以使用枚举的方式去获取这些信息，但是这样做的平均时间复杂度期望为O(n)，数据范围一大，这样的方式就基本稳稳的超时了。

于是，线段树应运而生。线段树是一种高级数据结构，基于二分思想，以O(logn)的时间进行区间查找与修改。

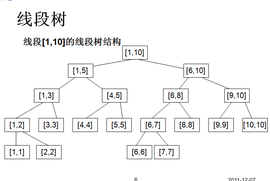
线段树常见的操作有：

1、建立一棵线段树(build)；
2、查询某区间的信息(ask)；
3、修改某个元素的值(replace)；
4、给某个区间内的元素全部加上一个值(add)。

（ps：代码中的p<<1、p<<1|1为位运算优化，效果等同于p*2,p*2+1。）

首先，我们来看看如何建立线段树。从上图来看，容易看出，线段树是一颗二叉树，每个节点都代表了一个区间，左孩子和右孩子都将父亲分为了两段。所以，我们可以采用二倍孩子法来储存。这里我采用了区间和线段树作为讲解模板。

template<typename T>//泛型，线段树内的元素可以指定类型
struct Tree
{
    int l,r;//该节点所管区间的左右边界
    T val;//这里保存的是将要查询的信息，如区间和、区间最值等。
}tree[SIZE<<2];

前面说了，线段树是基于二分思想的，所以，我们采用递归+分治的方式进行建树。

具体方式：

1、将区间边界赋给该节点；
2、如果左右边界相等，即区间内只有一个元素，则将数组内的值赋值给该叶节点，直接返回；
3、递归左孩子；
4、递归右孩子；
5、用左右孩子的信息来更新当前节点的信息。

代码：

void Build(int p,int l,int r,T *a)//p指的是当前的区间节点
{
    tree[p].l=l,tree[p].r=r;//1
    if(l==r){tree[p].val=a[l];return;}//2
    int mid=(l+r)>>1;
    Build(p<<1,l,mid,a);//3
    Build(p<<1|1,mid+1,r,a);//4
    tree[p].val=tree[p<<1].val+tree[p<<1|1].val;//5
}

然后，就是查询区间信息了。因为我们建树的时候已经把各个节点的信息更新好了，所以现在可以直接查找了。

具体步骤：

1、如果当前节点管辖区间正好等于查找区间，直接返回该节点的信息值；
2、如果当前节点的左孩子正好完全包含查找区间，则递归到左孩子查找；
3、如果当前节点的右孩子正好完全包含查找区间，则递归到右孩子查找；
4、如果查找区间在左孩子中有一部分，在右孩子中有一部分，则左右区间都递归查找，再根据需要的信息进行操作。

代码：

T Ask(int p,int l,int r)
{
    if(tree[p].l==tree[p].r){return tree[p].val;}
    int mid=(tree[p].l+tree[p].r)>>1;
    if(l<=mid&&r<=mid) return Ask(p<<1,l,r);
    else if(r>mid&&l>mid) return Ask(p<<1|1,l,r);
    else return Ask(p<<1,l,r)+Ask(p<<1|1,l,r);
}

然后，则是单点元素更改了。在理解完上面的内容后，单点更改就非常容易了。

具体步骤：

1、如果当前区间节点只有一个元素，且此元素为待修改元素，直接修改，返回；
2、如果节点在左区间，则递归左区间；
3、反之，递归右区间；
4、用左右节点信息更新当前节点信息。

代码：

void Replace(int p,int index,T val)
{
    if(tree[p].l==tree[p].r){tree[p].val=val;return;}//1
    int mid=(tree[p].l+tree[p].r)>>1;
    if(index>mid) Replace(p<<1|1,index,val);//2
    else Replace(p<<1,index,val);//3
    tree[p].val=tree[p<<1].val+tree[p<<1|1].val;//4
}

接下来，则是重头戏——区间整体增加（add）。

按照以上的方式，进行区间整体增加的方式只能是对区间内每个元素进行单点更改，共计length次修改，时间复杂度为O(nlogn)。对于某些题目，显然是不能满足速度需求的。那么，有更快的算法吗？

观察其他的线段树教学blog可以发现，在区间修改时，使用了一个叫lazytag，也就是懒标记的东西。为什么叫做懒标记？因为它很懒

我们给每个节点额外增加一个成员变量tag，也就是上述的“懒标记”。

struct Tree
{
    int l,r;
    T val,tag;//懒标记
}tree[SIZE<<2];

懒标记为什么叫做懒标记？因为它的作用是作为一个传递标记使用。在更改区间时，找到一个包含在待更改区间内的区间节点后，不继续向下更新，而是更新完自身后，只把增加值给懒标记。等到以后要访问下面的节点时，才将当前节点懒标记下传给下面的子节点。

这么一来，在区间修改操作中，我们的均摊复杂度就只有O(logn)了（常数比较大）。

值得注意的一点是，由于在调整区间值时，我们并没有把底下的区间更改，只是挂在了上面的lazytag上，所以在单点更改和获取信息时，记得要先将lazytag下放，再向下递归。

首先是下放的函数：
void Spread(int p) { if(tree[p].tag)//如果tag为0就没必要下放了 { int tag=tree[p].tag; //一个区间管n个元素，所以val要加上tag*n tree[p<<1].val+=tag*(tree[p<<1].r-tree[p<<1].l+1);//更新左子树 tree[p<<1|1].val+=tag*(tree[p<<1|1].r-tree[p<<1|1].l+1);//更新右子树 tree[p<<1].tag+=tag,tree[p<<1|1].tag+=tag;//下放 tree[p].tag=0;//tag下传完毕后就可以释放了 } }
然后是区间修改：

void Add(int p,int l,int r,T val)
{
    if(l<=tree[p].l&&r>=tree[p].r)//如果包含了待修改区间，直接修改tag和val，不再向下下传与递归。
    {
        tree[p].val+=val*(tree[p].r-tree[p].l+1);
        tree[p].tag+=val;
        return;
    }
    Spread(p);//下传懒标记
    int mid=(tree[p].l+tree[p].r)>>1;
    if(l<=mid) Add(p<<1,l,mid,val);//左递归
    if(r>mid) Add(p<<1|1,mid+1,r,val);//右递归
    tree[p]val=tree[p<<1].val+tree[p<<1|1].val;//更新节点信息
}

ask和replace只要在左右向下递归前下传tag就可以了。

线段树（SegmentTree）学习笔记

原文：https://www.cnblogs.com/MaxDYF/p/9780808.html