西瓜笔记(五上)--线性模型

一、基本形式

一个示例具有d个属性x=(x_1,x₂...x_d)。我们试图学习一个预测函数，即：

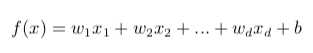
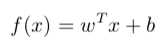
线性模型有很好的可解释性，直观地看出哪个属性的重要程度。

二、线性回归

1、代价函数(cost function)

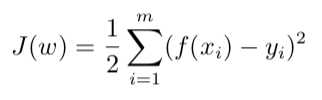
利用最小二乘法进行参数估计：

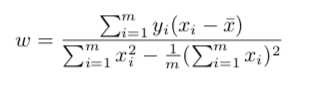
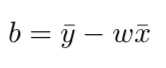
更一般的情形是，样本有d个属性描述，试图学得：

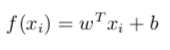
这称为“多元线性回归”。同样利用最小二乘法。将b吸收进w的向量中，数据集D是一个m*(d+1)大小的矩阵X，每行对应一个实例，每行最后一个元素为1：

此时的误差函数

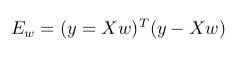
此为Frobenius范数：

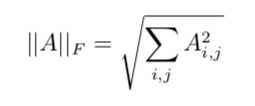
常用来衡量矩阵的大小。类似向量的L2范数。当X^TX为满秩矩阵或正定矩阵时：

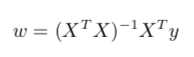
然而，现实生活中X^TX往往不是满秩矩阵，有些问题中属性的个数会超过我们的样例个数，导致会解出多个w，他们都能使均方误差最小化，选择哪一个就取决于学习算法的归纳偏好。常见的做法就是引入正则化。

三、广义线性模型

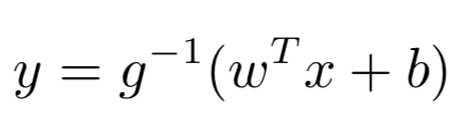
他们在形式上仍然是线性回归，但是实际上可以求取输入空间到输出空间的非线性函数映射。

对数几率回归就是其中的一种。它基于对数几率函数：

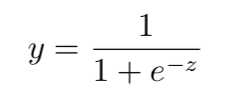
带入广义线性模型的通式得到：

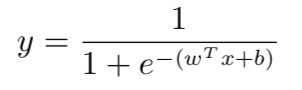
变化成：

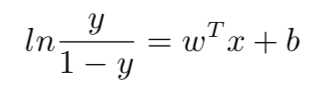
将y视为样本x作为正例的可能性，则1-y是其反例可能性，两者的比值是：

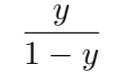
称上式为“几率（odds）”，对几率取对数得到的是“对数几率（log odds 亦称logit）”：

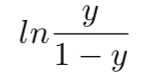
对数几率回归实际上是一种分类学习方法。对参数w和b的计算可以使用“极大似然法”。于是，重写上式得：

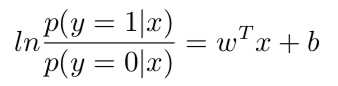
显然有：

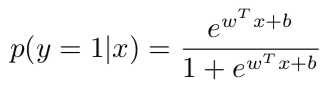
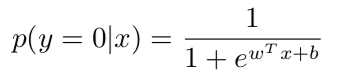
得到我们的对数似然函数：

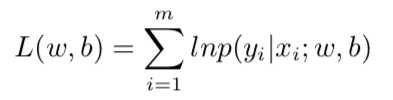
令：p1=p(y=1|x),p0=p(y=0|x)，重写似然项：

其中x‘和β是之前说过的吸收了b的w向量（增广矩阵），带入对数似然函数：

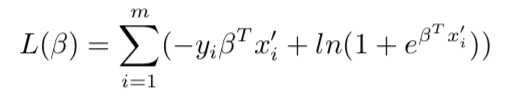
推导过程：

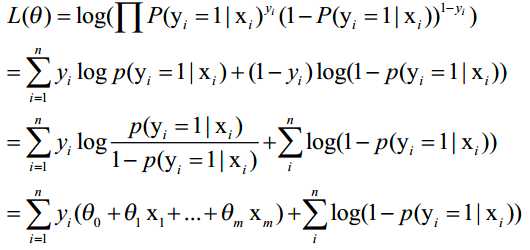
然后取反，那么，最大化log likelihood就相当于最小化上式。可以使用经典的数值优化算法，例如梯度下降法，牛顿法等。

西瓜笔记(五上)--线性模型

原文：https://www.cnblogs.com/melina-zh/p/9760943.html