Reference:
http://blog.csdn.net/rrerre/article/details/6751520
http://blog.csdn.net/y990041769/article/details/21026445
最大流Edmonds_Karp算法模板:
算法思想: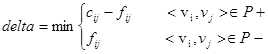
step 1. 令所有弧的流量为0,从而构造一个流量为0的可行流f(称作零流)。
step 2. 若f中找不到可改进路则转step 5;否则找到任意一条可改进路P。
step 3. 根据P求delta。
step 4. 以delta为改进量,更新可行流f。转step 2。
step 5. 算法结束。此时的f即为最大流。
算法的关键步骤是step 2,即:判断是否存在可改进路,若存在又如何求。
可以考虑用广度优先搜索。设置标志数组,记录顶点是不是被访问过;使用队列来存储已经访问过的顶点;另用一个一维数组p[i],记录每个顶点是由哪个顶点扩展而来(即记录父亲节点)。
首先S入队列。然后每次取队首顶点v,分析所有与v相邻的未访问顶点u:
1、存在弧<v, u>(正向弧),且u未访问。若f(v,u)<C(v,u)(非饱和弧),那么u入队列,给u打上“已访问”的标志,记u的父亲节点为v。
2、存在弧<u, v>(反向弧),且u未访问。若f(u,v) > 0(非零流弧),那么u入队列,给u打上“已访问”的标志,记u的父亲节点为-v。(以示和正向弧的区别)。
扩展完成后,若T还没有被访问就必然不存在可改进路;否则就从T出发,根据记录好的每个顶点的父亲节点信息,顺藤摸瓜,找出可改进路(同时还可以计算出delta)。
起点st,终点m

#include <iostream> #include <vector> #include <cstring> #include <queue> using namespace std; int n,m,st,en; int cap[300][300]; //cap[u][v]:边(u,v)上的最大流量 int flow[300][300]; //flow[u][v]:边(u,v)上当前的流量 int a[300]; //a[u]:访问标记,同时还记录下delta值 int p[300]; //记录父节点用 const int inf=100000000; int EK() //st-->m { queue<int> Q; memset(flow,0,sizeof(flow)); memset(p,-1,sizeof(p)); int f=0,minflow=inf; while(1) { memset(a,0,sizeof(a)); a[st]=inf; Q.push(st); while(!Q.empty()) { int u=Q.front();Q.pop(); for(int v=1;v<=m;v++) if(!a[v]&&cap[u][v]>flow[u][v]) { p[v]=u;Q.push(v); a[v]=a[u]<cap[u][v]-flow[u][v]?a[u]:cap[u][v]-flow[u][v]; } } if(a[m]==0) break; for (int u=m;u!=st;u=p[u]) { flow[p[u]][u]+=a[m]; flow[u][p[u]]-=a[m]; } f+=a[m]; } return f; } int main() { int S,E,C; while (cin>>n>>st>>m) //st->m { memset(cap,0,sizeof(cap)); for (int i=1;i<=n;i++) { cin>>S>>E>>C; cap[S][E]+=C; //处理重边。有些题目,一条路上先给了容量30,然后重复了一次50,这时候这条路上的容量应该是30+50。 } cout<<EK()<<endl; } return 0; }
模板例题:
hdu1532
-------------------------------------------------------------------------------------------
补充个ISAP模板,比EK算法快,但是难想难写。看不懂T^T...

#include <iostream> #include <cstdio> #include <climits> #include <cstring> #include <algorithm> using namespace std; typedef struct {int v,next,val;} edge; const int MAXN=20010; const int MAXM=500010; edge e[MAXM]; int p[MAXN],eid; void init(){memset(p,-1,sizeof(p));eid=0;} void insert1(int from,int to,int val) //有向 { e[eid].v=to;e[eid].val=val; e[eid].next=p[from]; p[from]=eid++; swap(from,to); e[eid].v=to;e[eid].val=0; e[eid].next=p[from]; p[from]=eid++; } void insert2(int from,int to,int val) //无向 { e[eid].v=to;e[eid].val=val; e[eid].next=p[from]; p[from]=eid++; swap(from,to); e[eid].v=to;e[eid].val=val; e[eid].next=p[from]; p[from]=eid++; } int n,m;//n为点数 m为边数 int h[MAXN]; int gap[MAXN]; int s,t; int dfs(int pos,int cost) { if (pos==t) return cost; int j,minh=n-1,lv=cost,d; for (j=p[pos];j!=-1;j=e[j].next) { int v=e[j].v,val=e[j].val; if(val>0) { if (h[v]+1==h[pos]) { if (lv<e[j].val) d=lv; else d=e[j].val; d=dfs(v,d); e[j].val-=d; e[j^1].val+=d; lv-=d; if (h[s]>=n) return cost-lv; if (lv==0) break; } if (h[v]<minh) minh=h[v]; } } if (lv==cost) { --gap[h[pos]]; if (gap[h[pos]]==0) h[s]=n; h[pos]=minh+1; ++gap[h[pos]]; } return cost-lv; } int isap(int st,int ed) { s=st;t=ed; int ret=0; memset(gap,0,sizeof(gap)); memset(h,0,sizeof(h)); gap[st]=n; while (h[st]<n) ret+=dfs(st,INT_MAX); return ret; } int main() { while(cin>>m>>n) { init(); for(int i=0;i<m;i++) { int u,v,c; scanf("%d%d%d",&u,&v,&c); insert1(u,v,c); } printf("%d\n",isap(1,n)); } return 0; }
原文:http://www.cnblogs.com/pdev/p/3873789.html