数据结构课上讲的KMP算法和我在ACM中学习的KMP算法是有区别的,这里我对课本上的KMP算法给出我的一些想法。
原理和之前的KMP是一样的https://www.cnblogs.com/wkfvawl/p/9768729.html,但是不同点在于之前的KPM中next数组存放的是到了该位时最大前后缀长度,而这里的KMP中next数组存放的是j下一步需要移动的位置。
“利用已经部分匹配这个有效信息,保持i指针不回溯,通过修改 j 指针,让模式串尽量地移动到有效的位置。”
所以,整个KMP的重点就在于当某一个字符与主串不匹配时,我们应该知道 j 指针要移动到哪?
接下来我们自己来发现j的移动规律:
如图:C和B不匹配了,我们要把 j 移动到哪?显然是第1位。为什么?因为前面有一个A相同啊:

如下图也是一样的情况:

可以把 j 指针移动到第2位,因为前面有两个字母是一样的:
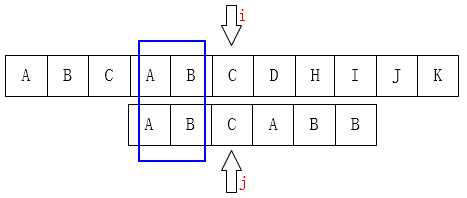
至此我们可以大概看出一点端倪,当匹配失败时,j要移动的下一个位置 k。
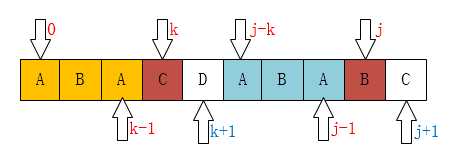
存在着这样的性质:最前面的k个字符和 j 之前的最后k个字符是一样的。
如果用数学公式来表示是这样的
P[0 ~ k-1] == P[j-k ~ j-1]
这个相当重要,如果觉得不好记的话,可以通过下图来理解:

弄明白了这个就应该可能明白为什么可以直接将 j 移动到 k 位置了。
因为:
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然:T[i-k ~ i-1] == P[0 ~ k-1]、
公式很无聊,能看明白就行了,不需要记住。
好,接下来就是重点了,怎么求这个(这些)k呢?
因为在P的每一个位置都可能发生不匹配,也就是说我们要计算每一个位置 j 对应的k,所以用一个数组next来保存,
介绍next:
(1)、j退到某next值时字符比较相等,指示器变量值各加1后继续比较;
(2)、next[j] = k,表示当 T[i] != P[j] 时,j 指针的下一个位置,也就是将要移动的位置
(3)、j退到-1的时候(即模式的第一个字符匹配失误时),i和j都要分别加1,表明从主串的下一个字符起和模式串进行匹配
(-1 只是定义的初值)
好,先把这个放一边,我们自己来推导思路,现在要始终记住一点,
next[j]的值(也就是k)表示,当P[j] != T[i]时,j指针的下一步移动位置。
先来看第一个:当j为0时,如果这时候不匹配,怎么办?
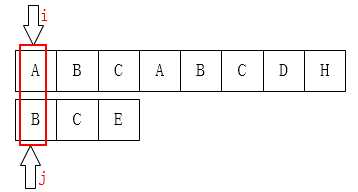
像上图这种情况,j已经在最左边了,不可能再移动了,这时候要应该是i指针后移。
如果是当j为1的时候呢?
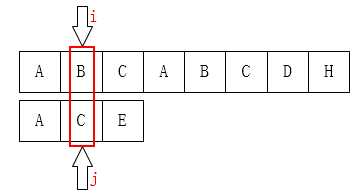
显然,j指针一定是后移到0位置的。因为它前面也就只有这一个位置了~~~
下面这个是最重要的,请看如下图:

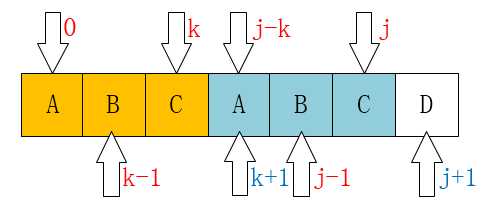
请仔细对比这两个图。
我们发现一个规律:
当P[k] == P[j]时,
有next[j+1] == next[j] + 1
其实这个是可以证明的:
因为在P[j]之前已经有P[0 ~ k-1] == p[j-k ~ j-1]。(next[j] == k)
这时候现有P[k] == P[j],我们是不是可以得到P[0 ~ k-1] + P[k] == p[j-k ~ j-1] + P[j]。
即:P[0 ~ k] == P[j-k ~ j],即next[j+1] == k + 1 == next[j] + 1。
这里的公式不是很好懂,还是看图会容易理解些。
那如果P[k] != P[j]呢?比如下图所示:
像这种情况,如果你从代码上看应该是这一句:k = next[k];为什么是这样子?你看下面应该就明白了。
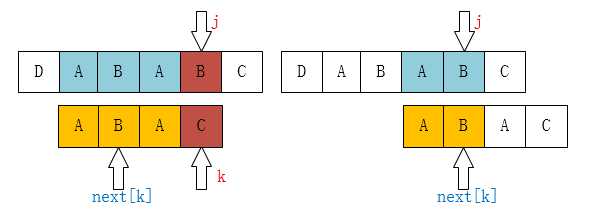
现在你应该知道为什么要k = next[k]了吧!像上边的例子,我们已经不可能找到[ A,B,A,B ]这个最长的后缀串了,但我们还是可能找到[ A,B ]、[ B ]这样的前缀串的。所以这个过程像不像在定位[ A,B,A,C ]这个串,当C和主串不一样了(也就是k位置不一样了),那当然是把指针移动到next[k]啦。
先看看next数据值的求解方法
位序 1 2 3 4 5 6 7 8 9
模式串 a b a a b c a b c
next值 0 1 1 2 2 3 1 2 3
next数组的求解方法是:
1.第一位的next值为0
2.第二位的next值为1
后面求解每一位的next值时,根据前一位进行比较
3.第三位的next值:第二位的模式串为b ,对应的next值为1;将第二位的模式串b与第一位的模式串a进行比较,不相等;则第三位的next值为1(其他情况均为1)
4.第四位的next值:第三位的模式串为a ,对应的next值为1;将第三位的模式串a与第一位的模式串a进行比较,相同,则第四位的next值得为1+1=2
5.第五位的next值:第四位的模式串为a,对应的next值为2;将第四位的模式串a与第二位的模式串b进行比较,不相等;第二位的b对应的next值为1,则将第四位的模式串a与第一位的模式串a进行比较,相同,则第五位的next的值为1+1=2
6.第六位的next值:第五位的模式串为b,对应的next值为2;将第五位的模式串b与第二位的模式中b进行比较,相同,则第六位的next值为2+1=3
7.第七位的next值:第六位的模式串为c,对应的next值为3;将第六位的模式串c与第三位的模式串a进行比较,不相等;第三位的a对应的next值为1,
则将第六位的模式串c与第一位的模式串a进行比较,不相同,则第七位的next值为1(其他情况)
8.第八位的next值:第七位的模式串为a,对应的next值为1;将第七位的模式串a与第一位的模式串a进行比较,相同,则第八位的next值为1+1=2
9.第八位的next值:第八位的模式串为b,对应的next值为2;将第八位的模式串b与第二位的模式串b进行比较,相同,则第九位的next值为2+1=3
如果位数更多,依次类推
1 void getNext(char *p,int *next) 2 { 3 int j,k; 4 next[1]=0; 5 j=1; 6 k=0; 7 while(j<strlen(p)-1) 8 { 9 if(k==0||p[j]==p[k]) //匹配的情况下,p[j]==p[k],next[j+1]=k+1; 10 { 11 j++; 12 k++; 13 next[j]=k; 14 } 15 else //p[j]!=p[k],k=next[k] 16 k=next[k]; 17 } 18 }
原文:https://www.cnblogs.com/wkfvawl/p/9794954.html