20181014NOIP模拟

SDOI模拟赛 #9

2018.10.14 8:00~11:30

Powered By _C_H_M_ , Marser

(Please Read The Instructions On This Page Carefully)

一、题目概览

二、注意事项

1. 文件名（源程序名和输入输出文件名）必须使用小写。

2. 评测在windows下lemon中进行。输入输出long long int 类型数值请使用cin/cout 或“%lld”。

3. main函数的返回值类型必须是int，程序正常结束时返回值必须是0。

4. 题目较水，请AK的同学不要D出题人，没AK的同学也不要D出题人。赛后会向AK的同学、前三名同学以及AC附加题的同学发放奖品。

5. 本次采用OI赛制，在比赛结束后统一交题，祝大家RP=INT_MAX。

第一题：

题目：

流星(meteor)

【题目背景】

我带着深藏骨血的仇恨与酝酿多年的阴谋

把自己变成一个死而复生的幽灵 沉入沼泽，沉入深渊

我想埋下腐烂的根系 长出见血封喉的荆棘 刺穿这个虚伪的文明

我到了淤泥深处…… 捡到了一颗星星。

晨光起于白塔尖顶，终将铺满阴霾之地。

【题目描述】

Marser正在和副词看星星。这时，他们发现了一颗流星划过天际。Marser出于习惯，记录下了这颗流星出现和消失的位置。Marser用两组坐标来描述这两个位置。你可以认为它们被Marser放在了一个原点由Marser指定的笛卡尔坐标系中。

现在，副词为了考验Marser的智商，想问他一个问题：按照Marser的坐标系定义，这颗流星一共经过了多少个格点？这里，格点被定义为坐标均为整数的点。

Marser用了1ms就完成了这个问题，于是他想用这个问题来测试您的智力。当然，为了简化您的操作，您可以把流星的运动轨迹看成一条直线。这样，您可以把这个问题转化为求一条线段除了端点外经过了多少个格点。

【输入格式】

从文件meteor.in中读入。

读入两行，每行两个整数x,y，表示线段的两个端点的坐标。

【输出格式】

输出到文件meteor.out中。

输出一行一个整数，表示除了两个端点外，线段经过的格点数量。

【输入输出样例】

【数据范围与约定】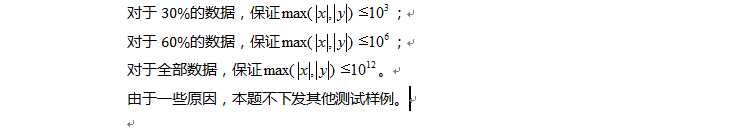

解析：

       我们想象把这条线段的一个端点已到原点，则另一点变为(x2-x1,y2-y1),所以这道题目就变为在函数y=(y2-y1)/(x2-x1)x中，(0<x<=x2-x1)找到有多少个整数x使得y也为整数，我们代入一个数值去算，那么必然是先将(y2-y1)/(x2-x1)化为最简形式，x2-x1/x2-x1(化解后)即为答案，其实这个值就是他们之前化解的倍数即为gcd（x2-x1,y2-y1）;

错点：

1、数据范围，注意使用long long定义；

2、特判端点重合，线段与x，y轴平行的情况

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#define ll    long long
using namespace std;
ll gcd(ll x,ll y){
    if(y>x)return gcd(y,x);
    if(y==0)return x;
    return gcd(y,x%y);
} 
int main(){
    freopen("meteor.in","r",stdin);
    freopen("meteor.out","w",stdout);
    ll x1,x2,y1,y2;
    cin>>x1>>y1>>x2>>y2;
    if(x1==x2&&y1==y2){printf("0");return 0;}
    x2-=x1;
    y2-=y1;
    if(x2<0)x2-=2ll*x2;
    if(y2<0)y2-=2ll*y2;
    ll d=gcd(x2,y2);
    if(y2==0)printf("%lld",x2-1);
    else if(x2==0)printf("%lld",y2-1);
    else printf("%lld",d-1);
    return 0;
} 

View Code

 第二题：

题目：

Hash键值（hash）

【题目背景】

所有的苦难与背负尽头，

都是行云流水般的此世光阴。

一生所渴求的，全都伤人至深。

而一生所憎恶的，全都令人魂牵梦萦。

【题目描述】

Marser沉迷hash无法自拔，然而他发现自己记不住hash键值了……

Marser使用的hash函数是一个单纯的取模运算，每一个数i被对应到i mod p。他现在有一个数列，他采用这种方法，把每一个数对应到一个键值i mod p。他想知道对于给定的模数p和键值r，所有对应到该键值的数的和为多少。同时，Marser可能会发现他的数列出了一些问题，所以他还想随时更改数列中任意一项的值。

现在Marser有q个请求，每个请求可能是修改或是询问。对于每一个询问，你需要给出正确的答案。如果你不能在1s内正确回答所有询问，Marser就会让hotwords把你给续了。

【输入格式】

从文件hash.in读入。

第一行两个整数n，q，表示数列长度和请求数量。

第二行n个整数，表示初始的序列。

接下来m行，每行三个整数opt，x，y；

若opt=1，则询问在mod x时，所有对应到键值y的数的和。

若opt=2，则将数列第x项修改为y。

【输出格式】

输出到文件hash.out中。

对于每个询问，输出相应的答案。

【输入输出样例1】

【输入输出样例2】

见下发文件中的hash2.in/ans。

该样例满足子任务二的性质。

【输入输出样例3】

见下发文件中的hash3.in/ans。

该样例满足子任务三的性质。

【数据范围与约定】

解析:

其实子任务1和2都较容易实现，(2尚未成功),而总体的解决方案其实是在这两个之间折中选择

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
using namespace std;
int n,m,q;
int a[101010],sum[1010][1010];
int opt,x,y;
int main(){
    freopen("hash.in","r",stdin);
    freopen("hash.out","w",stdout);
    scanf("%d%d",&n,&q);
    m=sqrt(n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        for(int j=1;j<=m;j++)sum[j][i%j]+=a[i];
    }
    int ans=0;
    while(q--){
        scanf("%d%d%d",&opt,&x,&y);
        if(opt==1){
            if(x<=m)printf("%d\n",sum[x][y]);
            else{
                ans=0;
                for(int i=y;i<=n;i+=x)
                    ans+=a[i];
                printf("%d\n",ans);
            }
        }
        else{
            for(int i=1;i<=m;i++)
                sum[i][x%i]=sum[i][x%i]-a[x]+y;
            a[x]=y;
        }
    }
    return 0;
}

View Code

20181014NOIP模拟

原文：https://www.cnblogs.com/linzeli/p/9795139.html