https://jzoj.net/senior/#main/show/5895

有一个好像比较显然的性质,就是每条边最多经过两次
那么我们考虑哪些边需要经过两次。我们把需要经过两次的边连一条重边,这样我们最终的答案就是新图中的最优的欧拉回路
换句话说,我们要把原图中的奇数度数的点两两匹配(一张无向图存在欧拉回路并且仅当每个点的度数都为偶数),在它们之间连边,显然这个连的边是它们在原图的最短路。因为边长的特殊定义,最短路一定是在最小生成树上的。
于是我们只需要考虑最小生成树树上哪些边需要重复连。
注意到上面那个每条边最多经过两次的性质,我们称最终匹配的两两奇数点之间的最短路为路径,也就是不存在一条边在两条路径上,因为肯定会有更优的情况,这样好像就证完了。看图理解一下
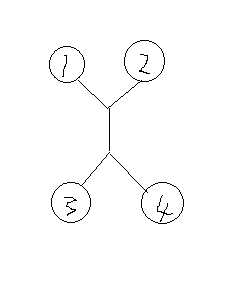
如果1,3匹配,2,4匹配的话,中间的边就在两条路径上,而我们显然可以更优的选择1,2匹配和3,4匹配
然后继续,我们发现最小生成树上的边是必须连的边并且仅当这条边两侧都有奇数个奇数度数的点,这样的边的边权我们计入路径和
最终答案就是路径和+所有边的边权和
#include<algorithm> #include<cstring> #include<iostream> #include<cstdio> #include<vector> using namespace std; typedef long long ll; const int N=5e5+15; const int mod=998244353; int n,m,ans; int h[N],fa[N],deg[N],siz[N],bin[N]; struct E{ int u,v,w; }e[N]; struct node{ int v,w; }; vector <node> mp[N]; inline int read(){ char ch=getchar();int s=0,f=1; while (ch<‘0‘||ch>‘9‘) {if (ch==‘-‘) f=-1;ch=getchar();} while (ch>=‘0‘&&ch<=‘9‘) {s=(s<<3)+(s<<1)+ch-‘0‘;ch=getchar();} return s*f; } int find(int x) {if (fa[x]!=x) fa[x]=find(fa[x]);return fa[x];} void dfs(int x,int pre){ siz[x]=deg[x]; for (int i=0;i<mp[x].size();i++){ int y=mp[x][i].v;if (y==pre) continue; dfs(y,x);siz[x]+=siz[y]; if (siz[y]&1) (ans+=bin[mp[x][i].w])%=mod; } } int main(){ freopen("travel.in","r",stdin); freopen("travel.out","w",stdout); n=read();m=read(); bin[0]=1;for (int i=1;i<=m;i++) (bin[i]=bin[i-1]<<1)%=mod; for (int i=1;i<=n;i++) fa[i]=i; for (int i=1;i<=m;i++) e[i].u=read(),e[i].v=read(),e[i].w=i,deg[e[i].u]^=1,deg[e[i].v]^=1,(ans+=bin[i])%=mod; for (int i=1;i<=m;i++){ int fx=find(e[i].u),fy=find(e[i].v); if (fx!=fy){ fa[fx]=fy; mp[e[i].u].push_back((node){e[i].v,e[i].w});mp[e[i].v].push_back((node){e[i].u,e[i].w}); } } dfs(1,0); printf("%lld\n",ans); return 0; }
[JZOJ 5895] [NOIP2018模拟10.5] 旅游 解题报告 (欧拉回路+最小生成树)
原文:https://www.cnblogs.com/xxzh/p/9802087.html