Given an undirected graph, return true if and only if it is bipartite.
Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
Example 2: Input: [[1,2,3], [0,2], [0,1,3], [0,2]] Output: false Explanation: The graph looks like this: 0----1 | \ | | \ | 3----2 We cannot find a way to divide the set of nodes into two independent subsets.
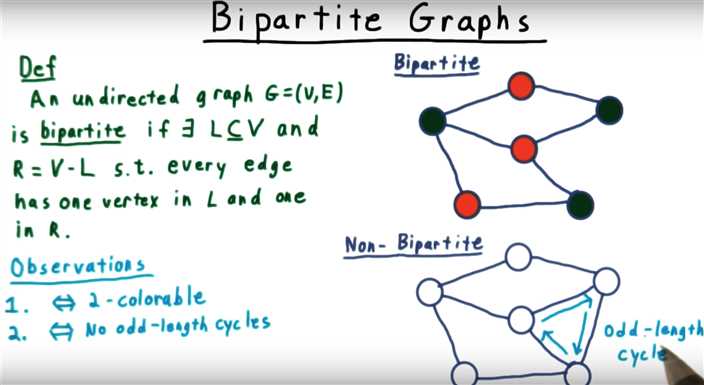
设G=(V,E)是一个无向图。如顶点集V可分割为两个互不相交的子集V1,V2之并,并且图中每条边依附的两个顶点都分别属于这两个不同的子集
思路
1. based on Graph Bipartite attribute, we can fill two different color for each subset.
2. if not Graph Bipartite, at lease one node such that its color happens to be the same as its neighbor
3. coz we need to traversal each node, we can both use dfs and bfs
代码
1 class Solution { 2 public boolean isBipartite(int[][] graph) { 3 int[] visited = new int[graph.length]; 4 //default 0: not visited; 5 //lable 1: green 6 //lable 2: red 7 for(int i = 0; i < graph.length; i++) { 8 // such node has been visited 9 if(visited[i] != 0) {continue;} 10 //such node has not been visited 11 Queue<Integer> queue = new LinkedList(); 12 queue.add(i); 13 // mark as green 14 visited[i] = 1; 15 while(!queue.isEmpty()) { 16 int cur = queue.poll(); 17 int curLable = visited[cur]; 18 // if curLable is green, fill neighborLable to red 19 int neighborLable = curLable == 1? 2:1; 20 for(int neighbor:graph[cur]) { 21 //such node has not been visited 22 if(visited[neighbor] == 0) { 23 visited[neighbor] = neighborLable; 24 queue.add(neighbor); 25 } 26 // node visited, and visited[neighbor] != neighborLable, conflict happens 27 else if(visited[neighbor] != neighborLable) { 28 return false; 29 } 30 } 31 } 32 } 33 return true; 34 } 35 }
[leetcode]785. Is Graph Bipartite? [bai'pɑrtait] 判断二分图
原文:https://www.cnblogs.com/liuliu5151/p/9814350.html