Problem Description
A school bought the first computer some time ago(so this computer‘s id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.
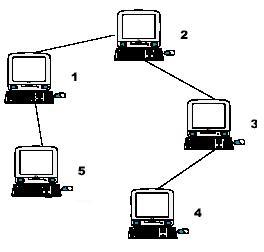
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.
Input
Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.
Output
For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).
Sample Input
5 1 1 2 1 3 1 1 1
Sample Output
3 2 3 4 4
::所有电脑连接成树形结构,要求求出每个结点到离该结点最远距离。
如果以每个结点为根结点,进行一次dfs,那就很容易求出那个最远距离。但是如果只是单纯的暴力,时间是不够的,
不过我们可以用DP的思想,避免计算重复的子问题,利用这个剪枝,效率就相当高。
我的实现方法:以每个结点为根结点root,进行一次dfs,用dp保存的是经过某条边能到达的最远距离。
边的保存是双向的,给每条边一个序号。//下面dp[x], x就是边的序号
以上图为例,首先选取任意一结点这里选1,为根结点,进行dfs,然后我们就可以求出经过边2边1..边4….所能到达的最远距离dp[1], d[2]……dp[4]..
然后以2为根结点dfs, 因为经过边4所能到达最远距离dp[4]以知道。。dp[7], dp[2]也知道,那离结点2最远结点的距离等于max(dp[4], dp[7], dp[2]+dis[3]),//dis[3]表示第三条边的长度
view code
hdu 2196 Computer(树形DP),布布扣,bubuko.com
原文:http://www.cnblogs.com/zyx1314/p/3874872.html