回归分析:在一系列已知自变量与因变量之间相关关系的基础上,建立变量之间的回归方程,把回归方程作为算法模型,实现对新自变量得出因变量的关系。
回归与分类的区别:回归预测的是连续变量(数值),分类预测的是离散变量(类别)。
设有特征值x1、x2(二维),则预测值 $ h_\theta(x)=\theta_0 + \theta_1x_1 + \theta_2x_2 $
写为矩阵形式:令x0为全为1的向量,$ h_\theta(x)=\sum_{i=0}^n\theta_i x_i =\theta^T x$
真实值和预测值之间的偏差用 \(\varepsilon\) 表示,则有 $ y^{(i)} = \theta^Tx^{(i)} + \varepsilon^{(i)}$
假设 误差\(\varepsilon^{(i)}\)是独立同分布的 通常认为服从均值为 \(0\) 方差为 \(\sigma^2\) 的正态分布
\[ \begin{split} &p(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(\epsilon^{(i)})^2}{2\sigma^2}} \则有&p(y^{(i)}\mid x^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \\end{split} \]
p(x|theta)表示条件概率,是随机变量
p(x;theta)表示待估参数(固定的,只是当前未知),可直接认为是p(x),加了分号是为了说明这里有个theta参数
用极大似然估计求\(\theta\),
\[
L(\theta)=\prod_{i=1}^mp(y^{(i)}\mid x^{(i)};\theta)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}}
\]
\[
\begin{split}
l(\theta)&=\log L(\theta)\&=\log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \&= \sum_{i=1}^m\log\frac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{( y^{(i)}-\theta^Tx^{(i)} )^2}{2\sigma^2}} \&= m\log\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{2\sigma^2}\sum_{i=1}^m(y^{(i)}-\theta^Tx^{(i)})^2\\end{split}
\]
化为求目标函数\(J(\theta)=\dfrac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2\)的最小值。
化为用矩阵形式表示:
\[
J(\theta)=\frac{1}{2}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2
=\frac{1}{2}(X\theta-y)^T(X\theta-y)
\]
然后对\(\theta\)求导:
\[
\begin{split}
\triangledown_\theta J(\theta)&=\triangledown_\theta(\frac{1}{2}(X\theta-y)^T(X\theta-y))\&=\triangledown_\theta(\frac{1}{2}(\theta^TX^T-y^T)(X\theta-y))\&=\triangledown_\theta(\frac{1}{2}(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty))\&=\frac{1}{2}(2X^TX\theta-X^Ty-(y^TX)^T)\&=X^TX\theta-X^Ty
\end{split}
\]
令 \(X^TX\theta-X^Ty=0\),则有最终结果 \(\theta = (X^TX)^{-1}X^Ty\)
上述方法有时候会出现不能直接求出极值的情况,比如矩阵不可逆,只能通过不断优化的过程求解。梯度下降顾名思义,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度,然后朝着梯度相反的方向,就能让函数值下降的最快。
设 \(h_\theta(x)=\theta_1x+\theta_0\),
\[ \begin{split} J(\theta_0,\theta_1)&=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2\\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})\\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} &= \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})x_i\\end{split} \]
更新后的\(\theta_0,\theta_1\)(选取合适的\(\alpha\)做步长):
\[ \begin{split} \theta_0:=\theta_0-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0}\\theta_1:=\theta_1-\alpha*\frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} \end{split} \]
Sigmoid函数 \(g(x) = \dfrac{1}{1+e^{-x}}\)将任意实数x映射到(0,1)区间
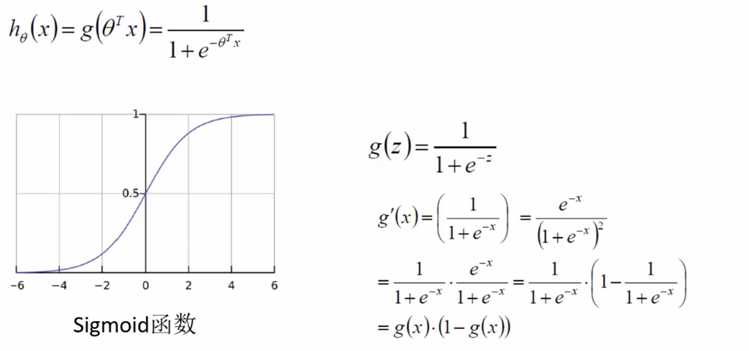
原文:https://www.cnblogs.com/thousfeet/p/9830258.html