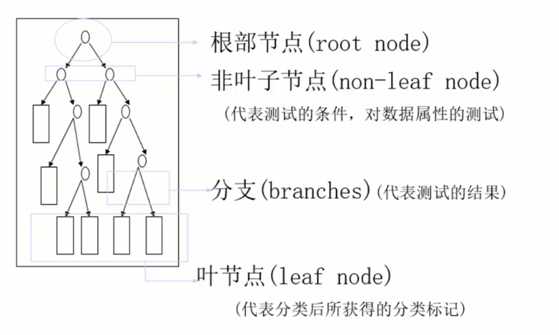
决策树算法以树状结构表示数据分类的结果。每个决策点实现一个具有离散输出的测试函数,记为分支。
一棵决策树的组成:根节点、非叶子节点(决策点)、叶子节点、分支
算法分为两个步骤:1. 训练阶段(建模) 2. 分类阶段(应用)
设用P(X)代表X发生的概率,H(X)代表X发生的不确定性
-> P(X)越大,H(X)越小;P(X)越小,H(X)越大
熵 =$ -\sum_{i=1}^nP_i\log(P_i)$
信息熵的一句话解释是:衡量信息消除不确定性的程度。因此,当熵较小时表示集合较纯,分类效果比较好。
构造树的基本想法是随着树深度的增加,节点的熵迅速的降低,降低的速度越快越好,这样才有望得到一棵高度最矮的决策树。
如何选取根节点:选取 信息增益=划分前熵值-划分后熵值 最大的
ID3:信息增益
C4.5:信息增益率
CART:Gini系数
Gini系数 \(Gini(p)=\sum_{k=1}^Kp_k(1-p_k)=1-\sum_{k=1}^Kp^2\) 同样是值较小时分类效果好
使用传统信息增益做划分的问题:当存在一些属性很多、每个属性对应的样本数据很少的特征(如id值),会出现信息增益大,但其实和样本的划分关系不大的问题。-> 引入信息增益率(增益率除以划分前的熵值)
评价函数:\(C(T)=\sum_{t\in leaf}N_t*H(t)\) ,\(H(t)\)表示熵值或系数值,\(N_t\)表示叶节点中的样本数 (评价函数值越小越好)
如何处理连续型的属性:离散化,将连续型属性的值分为不同的区间,依据是比较各个分裂点Gain值的大小
缺失数据的考虑:忽略,即在计算增益时,仅考虑那些具有属性值的记录
决策树太高 分支太多 -> 很容易过拟合(在训练集上划分为100% 但在测试集上效果不好) -> 剪枝
预剪枝:在构建决策树的过程中,提前停止。如限制深度、限制当前集合的样本个数的最低阈值。
后剪枝:在决策树构建好后才开始剪枝。如重新定义评价函数 \(C_\alpha(T)=C(T)+\alpha\cdot\mid T_{leaf}\mid\)(限制叶子节点个数,手动设置\(\alpha\)以控制影响程度),构建之后对每个节点比较剪枝和不剪枝的效果
采样方式:
Bootstraping:有放回采样
Bagging:有放回采样,一共建立n个分类器
随机:
[ML学习笔记] 决策树与随机森林(Decision Tree&Random Forest)
原文:https://www.cnblogs.com/thousfeet/p/9830541.html