一、前言
昨晚下班后,经理出于兴趣给我们技术组讲了讲算法相关的东西,全程一脸懵逼的听,中途还给我们出了一道比较有趣的爬楼问题,问题如下:
假设一个人从地面开始爬楼梯,规定一步只能爬一坎或者两坎,人只能往上走,例如爬到第一坎,很明显从地面到第一坎只有一种可选方式,从地面爬到第二坎,他可以从地面直接跨到第二坎,也可以先从地面到第一坎,再从第一坎到第二坎,也就是2种可选方式,那么求他爬到N楼一共有几种可选方式。
这道题涉及到了斐波那契数列,要求使用递归来求值,技术贼菜的我也是一脸懵逼,所以本着学习的心还是记录下来了。
二、有趣的斐波那契数列
我们将地面理解为数字0,第一坎理解为数字1,以此来进行简单的分析:
例如从0到1,就一种选择,如图(公司不让用破解软件,没PS画图,凑合看吧,画图的手微微颤抖。。。)
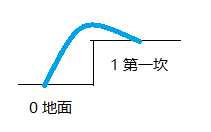
那么,现在要求到第二坎,从0到2呢,两种选择,看图分析(记住,一步只能跨一坎或者两坎):
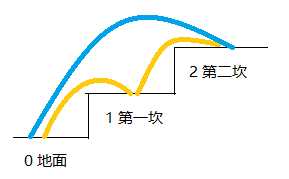
当要求从0到3,三种选择,如图:
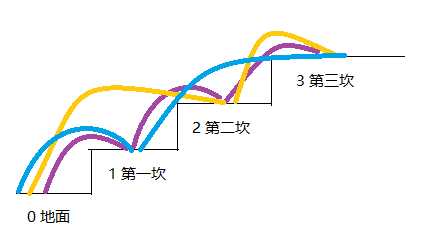
紫色:一坎坎的走;黄色:先走两坎,再走一坎;蓝色:先走一坎,再走两坎。
从0-4,一共五种情况,如图:
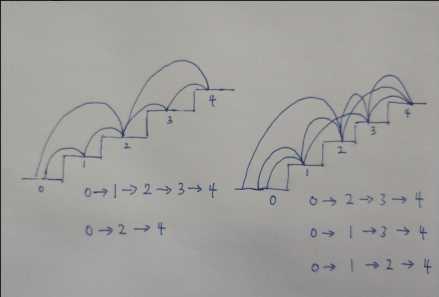
这里我分开画了,左边的2种情况加上右边的三种情况
左边:
第一种:一坎坎的走,0-1-2-3-4
第二种:两坎两坎走,0-2-4
右边:
第三种:先走两坎,再一坎坎的走0-2-3-4
第四种:先走一坎,再走两坎,再走一坎0-1-3-4
第五种:先走一坎,再走一坎,再走两坎0-1-2-4
当我们继续往后画,楼梯层对应走法会形成一个有趣的规律,
从第三层开始,第三层的走法等于一层与二层走法的和,第四层的走法等于第二层和第三层走法的和.....针对楼梯问题,我们可以得到如下公式:
F(n) = F(n-1) + F(n-2) n>=3
这就是著名的斐波那契数列(Fibonacci sequence),又称黄金分割数列。有兴趣的同学可以查查兔子繁殖问题。
百科里斐波那契数列的基数n>=4是根据实际情况来定的,这点不用纠结。
三、斐波那契数列与递归的结合
什么是递归?自己调用自己的函数就是递归,这么说完全没问题。
我们回归上面的问题,要求第N层的走法,那我们只需要知道N-1层和N-2层的走法就好了,假设N是10,求到第十层的走法。
十层走法=九层的走法+八层走法
九层和八层也可以拆分啊,九层走法 = 七层走法 + 八层走法 ,而八层走法 = 七层走法 + 六层走法
.......
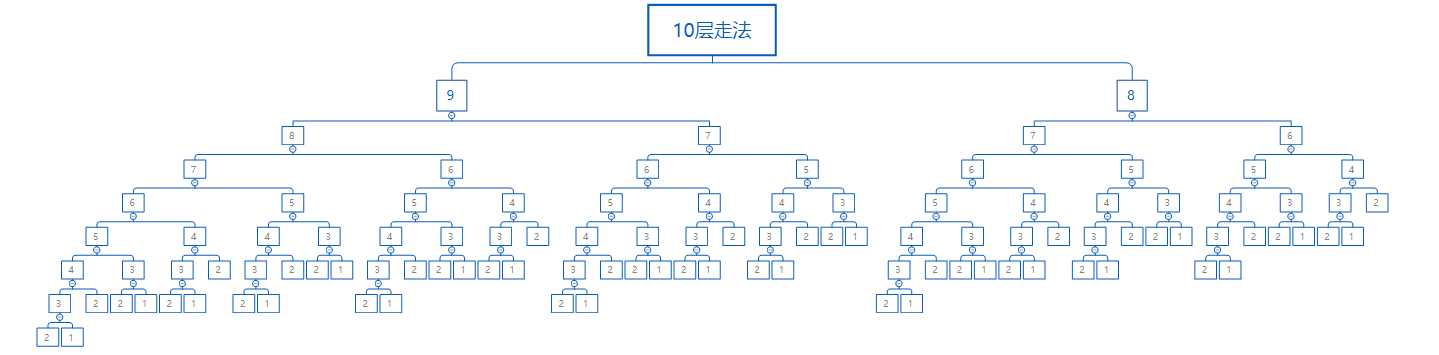
当分到3层时,最后还可以拆分为1层+2层,因为规律是从第三层开始的,因为此公式不适用于1层和2层,分到1层和2层就代表分支的结束了。
使用闭包需要找到跳出自己调用自己的的临界条件,不然会会陷入死循环,那对应我们的楼梯问题,只要N<3时就不需要继续调用自己了,因为不需要继续产生分支了。
这个闭包怎么写呢?我们结合斐波那契数列公式尝试一下吧。
现在有一个函数,里面申明一个走法变量var step = 0;输入一个数字N,我们会对N判断,只要N>=3,它就会自己调用自己,小于3时,我们分别判断它等于1或者2,等于1就让step加1,等于2就让step加2,如下:
function recursion(n){ let step = 0; if (n === 1 ){ step += 1 }else if (n === 2){ step += 2; }else if (n >= 3){ step = recursion(n-1) + recursion(n-2); }; return step; }; console.log(recursion(10))//89种
为了验证,我将上方分支图中所有的1与2相加(1层只有1种走法,2层有2种),得出数字也确实是89。所以我不明白我为什么要把基数N设置为10,算的难受。
那么趁热打铁,活学活用,现在我们尝试求正整数N与N之前所有正整数累加的和。
例如3之前累加的和就是3+2+1,数字0加不加没意义,所以跳出递归的临界条件就是当N>=2时,最后调用一次让之前数字的和加一次1就好了。
var result = 0; function add(n){ result += n n>=2 ? add(n-1) : null; return result; }; console.log(add(10));//55
验证一下,完全没问题,有没有觉得递归挺简单。
当你看到这时,恭喜你,不仅了解了斐波那契数列,也简单了解了递归的用法。其实本人在工作中需要操作数据,本能的总是想到穷举,循环,那么现在又多了一种可行的解决方法,也算是对于思维的开拓了。
留个问题,回到上方两段实现代码,为什么第一个变量申明在函数体内,而第二个数字累加的变量申明要在函数体外呢?尝试思考下。
当然,前提是,这篇博客如果有人愿意看完就挺好了。

原文:https://www.cnblogs.com/echolun/p/9852528.html