小T 是一名质量监督员,最近负责检验一批矿产的质量。这批矿产共有 nn 个矿石,从 11到nn逐一编号,每个矿石都有自己的重量 w_iwi? 以及价值v_ivi? 。检验矿产的流程是:
1 、给定mm个区间[L_i,R_i][Li?,Ri?];
2 、选出一个参数WW;
3 、对于一个区间[L_i,R_i][Li?,Ri?],计算矿石在这个区间上的检验值Y_iYi?:
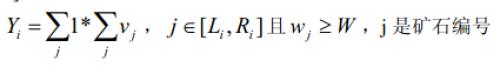
这批矿产的检验结果YY 为各个区间的检验值之和。即:Y_1+Y_2...+Y_mY1?+Y2?...+Ym?
若这批矿产的检验结果与所给标准值SS 相差太多,就需要再去检验另一批矿产。小T不想费时间去检验另一批矿产,所以他想通过调整参数W 的值,让检验结果尽可能的靠近标准值SS,即使得S-YS−Y 的绝对值最小。请你帮忙求出这个最小值。
11年的day2T2,需要一点思维和数学
首先我遇到的第一个难点是看不懂那个表达式
其实很简单,意思就是在这个区间内,重量小于W的东西的价值的和,再乘上其数量
然后我们会发现,Y的值是由W的值来决定的,随着W的增大而减小
要求的又是极值,所以自然而然的想到二分,
接下来就是如何判断了,因为是区间求和,而有时多个区间,肯定不能暴力
要用到的是前缀和优化,区间和和区间个数都能求
时间复杂度就是O(mlogw)的
别忘了开long long
下面给出代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #include<cmath> #include<algorithm> using namespace std; inline long long rd(){ long long x=0,f=1; char ch=getchar(); for(;!isdigit(ch);ch=getchar()) if(ch==‘-‘) f=-1; for(;isdigit(ch);ch=getchar()) x=x*10+ch-‘0‘; return x*f; } inline void write(long long x){ if(x<0) putchar(‘-‘),x=-x; if(x>9) write(x/10); putchar(x%10+‘0‘); return ; } long long n,m,s; long long w[1000006],v[1000006]; long long x[1000006],y[1000006]; long long sum[1000006]; long long cnt[1000006]; long long check(long long k){ memset(sum,0,sizeof(sum)*2); for(long long i=1;i<=n;i++){ sum[i]=sum[i-1],cnt[i]=cnt[i-1]; if(w[i]>=k) sum[i]+=v[i],cnt[i]+=1; } //for(long long i=1;i<=n;i++){ //cout<<sum[i]<<" "; //} long long num=0; for(long long i=1;i<=m;i++){ num+=(cnt[y[i]]-cnt[x[i]-1])*(sum[y[i]]-sum[x[i]-1]); //cout<<num<<endl; } return num; } int main(){ n=rd(),m=rd(),s=rd(); long long l=0x7ffffffffffff,r=0; for(long long i=1;i<=n;i++){ w[i]=rd(),v[i]=rd(); r=max(w[i],r),l=min(l,w[i]); } for(long long i=1;i<=m;i++) x[i]=rd(),y[i]=rd(); r++,l--; long long ans=0x7ffffffffffff; //write(check(4)); while(l<=r){ long long mid=(l+r)>>1; long long h=check(mid); if(abs(h-s)<ans) ans=abs(h-s); if(h>s) l=mid+1; else r=mid-1; } write(ans); return 0; }
原文:https://www.cnblogs.com/WWHHTT/p/9866980.html