Bezier曲线是应用于二维图形的曲线。曲线由顶点和控制点组成,通过改变控制点坐标可以改变曲线的形状。
一次Bezier曲线公式:
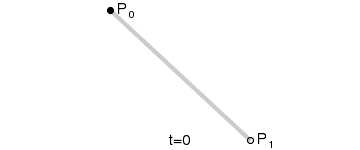
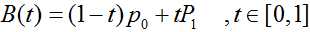
一次Bezier曲线是由P0至P1的连续点,描述的一条线段
二次Bezier曲线公式:
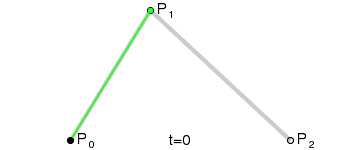
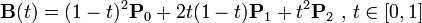
二次Bezier曲线是 P0至P1 的连续点Q0和P1至P2 的连续点Q1 组成的线段上的连续点B(t),描述一条抛物线。
三次Bezier曲线公式:
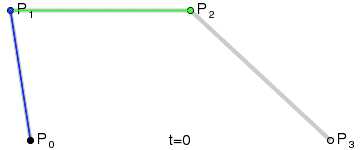
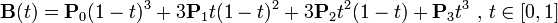
#include <vector> class CBezierCurve { public: CBezierCurve(); ~CBezierCurve(); void SetCtrlPoint(POINT& stPt); bool CreateCurve(); void Draw(CDC* pDC); private: // 主要算法,计算曲线各个点坐标 void CalCurvePoint(float t, POINT& stPt); private: // 顶点和控制点数组 std::vector<POINT> m_vecCtrlPt; // 曲线上各点坐标数组 std::vector<POINT> m_vecCurvePt; };
#include <math.h> #include "BezierCurve.h" CBezierCurve::CBezierCurve() { } CBezierCurve::~CBezierCurve() { } void CBezierCurve::SetCtrlPoint(POINT& stPt) { m_vecCtrlPt.push_back(stPt); } void CBezierCurve::CreateCurve() { // 确保是二次曲线,2个顶点一个控制点 assert(m_vecCtrlPt.size() == 3); // t的增量, 可以通过setp大小确定需要保存的曲线上点的个数 float step = 0.01; for (float t = 0.0; t <= 1.0; t += step) { POINT stPt; CalCurvePoint(t, stPt); m_vecCurvePt.push_back(stPt); } } void CBezierCurve::Draw(CDC* pDC) { // 画出曲线上个点,若不连续可以用直线连接各点 int nCount = m_vecCurvePt.size(); for (int i = 0; i < nCount; ++i) { pDC->SetPixel(m_vecCurvePt[i], 0x000000); } } void CBezierCurve::CalCurvePoint(float t, POINT& stPt) { // 确保是二次曲线,2个顶点一个控制点 assert(m_vecCtrlPt.size() == 3); // 计算曲线点坐标,此为2次算法,改变此处可以实现多次曲线 float x = (float)m_vecCtrlPt[0].x * pow(1 - t, 2) + (float)m_vecCtrlPt[1].x * t * (1 - t) * 2 + (float)m_vecCtrlPt[2].x * pow(t, 2); float y = (float)m_vecCtrlPt[0].y * pow(1 - t, 2) + (float)m_vecCtrlPt[1].y * t * (1 - t) * 2 + (float)m_vecCtrlPt[2].y * pow(t, 2); stPt.x =x; stPt.y= y; }
Bezier贝塞尔曲线的原理、二次贝塞尔曲线的实现,布布扣,bubuko.com
原文:http://www.cnblogs.com/hyb1/p/3875468.html