有这么一个问题, 给定一个数(假定32位), 如何得到这个数转为二进制后1的个数?
解:
X=(x & 0x55555555)+((x>>1)&0x55555555)
X=(x & 0x33333333)+((x>>2)&0x33333333)
X=(x & 0x0F0F0F0F)+((x>>4)& 0x0F0F0F0F)
X=(x & 0x0000FFFF)+((x>>1)& 0x0000FFFF)
原理图:
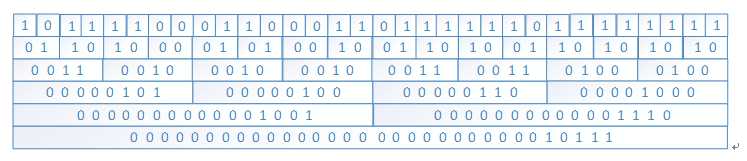
将原始问题(统计32个位元中1的个数),分解为统计16个位元中1的个数,在分解为统计8个位元中1的个数……, 最后统计两个位元中1的个数。最后求和。
分析:
首先请看左上角:
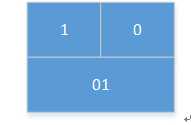
这两个位元中只有一个位元为1,于是将结果填写到下面的格子中。这一行以此类推。
接下来看第二行第三行:
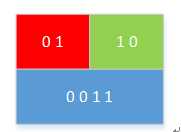
红色表示我的上面两个位元中只有一个位元为1,青黄色表示我的上面有两个位元为1,将两个数相加得到0011,代表我上面的4个位元中有3个位元为1.
.
.
.
以此类推, 得到最后的数为 0B010111 = 23
那么现在的问题是, 如何统计1的个数然后相加呢?
首先第一行, 0x55555555 = 0B01010101010101010101010101010101
与x与的结果就将偶数位的1取了出来, x>>1与0x55555555相与,就将奇数位的1取了出来。这两个数相加, 就将每两位中的1的个数取了出来,放到了下一行的对应的位中。
请注意,由于只右移了一位,因此只是统计每两位中的1的个数 。 可以使用1111&0101测试,很容易发现问题。
0x33333333 = 00110011001100110011001100110011
与x与的结果就所有第2^n和(2^n)-1的数取出来。与x>>2相与,就是将剩余的数取出来。,这些数就是位元为1个数的和。同样可以使用 1111&0011测试。
.
.
.
.
依次类推,最终得到的就是位元为1的个数。
统计值为1的位元数有很多方法,这里只是一种较为简单的分治法。还有很多精妙绝伦的方法。
参考文献:
<<算法心得(Hacker’s Delight)>> --机械工业出版社
原文:https://www.cnblogs.com/syyxy/p/9893204.html