特点:
There are n coins in a line. Two players take turns to take a coin from one of the ends of the line until there are no more coins left. The player with the larger amount of money wins.
Could you please decide the first player will win or lose?
Have you met this question in a real interview? Yes
Example
Given array A = [3,2,2], return true.
Given array A = [1,2,4], return true.
Given array A = [1,20,4], return false.
来来来, 先画个图: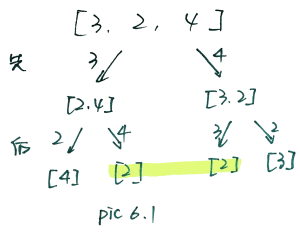
如图, 我们发现, 一下相同的重复的[2], 可以用记忆花搜索. 但是, 假设我们用一个状态dp[1], 我们不知道剩的一个, 是2, 是3还是4啊. 因为现在取一个硬币,可以从左边取, 也可以从右边取, 是有方向性的, 所以不能用dp[i]表示.
现在我们呢, 用一个区间的两个下标表示
public class Solution {
/**
* @param values: an array of integers
* @return: a boolean which equals to true if the first player will win
*/
public boolean firstWillWin(int[] values) {
// write your code here
int n = values.length;
int[] sum = new int[n + 1];
sum[0] = 0;
for (int i = 1; i <= n; ++i)
sum[i] = sum[i - 1] + values[i - 1];
// s[i][j] = sum[j + 1] - sum[i];
int[][] dp = new int[n][n];
for (int i = 0; i < n; ++i)
dp[i][i] = values[i];
for (int len = 2; len <= n; ++len) {
for (int i = 0; i < n; ++i) {
int j = i + len - 1;
if (j >= n)
continue;
int s = sum[j + 1] - sum[i];
dp[i][j] = Math.max(s - dp[i + 1][j], s - dp[i][j - 1]);
}
}
return dp[0][n - 1] > sum[n] / 2;
}
}
// 方法一
import java.util.*;
public class Solution {
/**
* @param values: an array of integers
* @return: a boolean which equals to true if the first player will win
*/
public boolean firstWillWin(int[] values) {
// write your code here
int n = values.length;
int [][]dp = new int[n + 1][n + 1];
boolean [][]flag =new boolean[n + 1][n + 1];
int sum = 0;
for(int now : values)
sum += now;