短, 小, 最问题
而90%DFS的题, 要么是排列, 要么是组合
问题模型:求出所有满足条件的“组合”
判断条件:组合中的元素是顺序无关的
时间复杂度:与 2^n 相关
一般来说,如果面试官不特别要求的话,DFS都可以使用递归(Recursion)的方式来实现。
递归三要素是实现递归的重要步骤:
? 递归的定义
? 递归的拆解
? 递归的出口
Given a set of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
The same repeated number may be chosen from C unlimited number of times.
如果有0:
取一次是一种方案, 取两次是一种方案, 最后有无数种方案.
看到新题要和老题产生关系, 哪儿像哪儿不像
这道题和subset的关系:
限制了一个和
去重: {1,2} == {2,1} 选代表
{2,2,3} = {2,3,2] = {3,2,2]
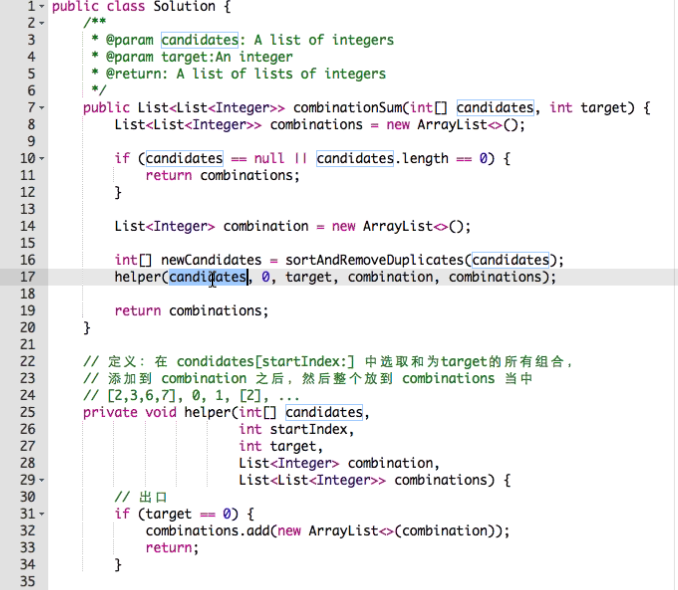
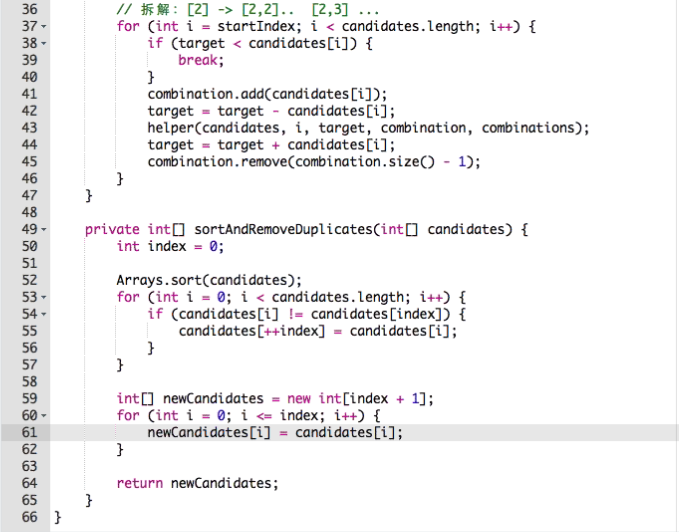
其中49行, [2’,2”,3]可能有三种:
[2’,2”,3]
[2’,2’,3]
ps: 也可以用hash set去重
Given an array of integers, remove the duplicate numbers in it.
You should:
Move the unique numbers to the front of the array.
Return the total number of the unique numbers.
class Solution {
public:
/**
* @param A: a list of integers
* @return : return an integer
*/
int removeDuplicates(vector<int> &nums) {
if (nums.size() == 0) {
return 0;
}
int len = 0;
for (int i = 1; i < nums.size(); i++) {
if (nums[len] != nums[i]) {
nums[++len] = nums[i];
}
}
return len + 1;
}
};两点需要注意:
return的不是index,二是数量,所以要加1
答案个数不知道, 假设为S;
每个答案用的时间=target;
所以总的时间复杂度= O(S*target), 是个NP问题
Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.
Each number in C may only be used once in the combination.
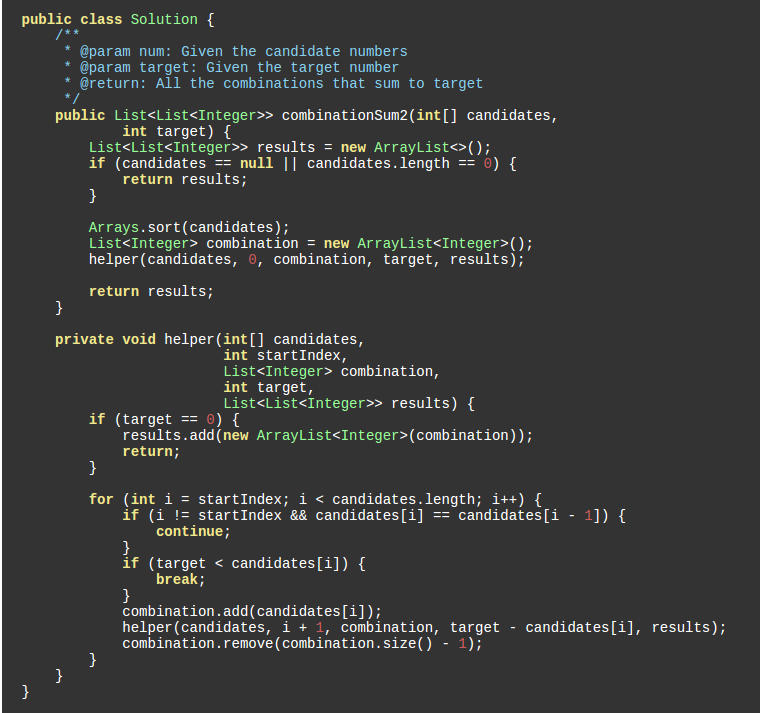
其中:
if (i != startIndex && candidates[i] == candidates[i - 1]) {
continue;
}去重的方式是相同的从第一个开始选, 不能跳过第一个选第二个.
Given a string s, partition s such that every substring of the partition is a palindrome.
Return all possible palindrome partitioning of s.
这道题的本质是组合问题:
aab怎么分割的问题, 就是要不要缝隙
三个字符两个空隙, 每个空隙我可以选择要或者不要, 所以有4个答案.

一边切, 一边验证是不是回文串:
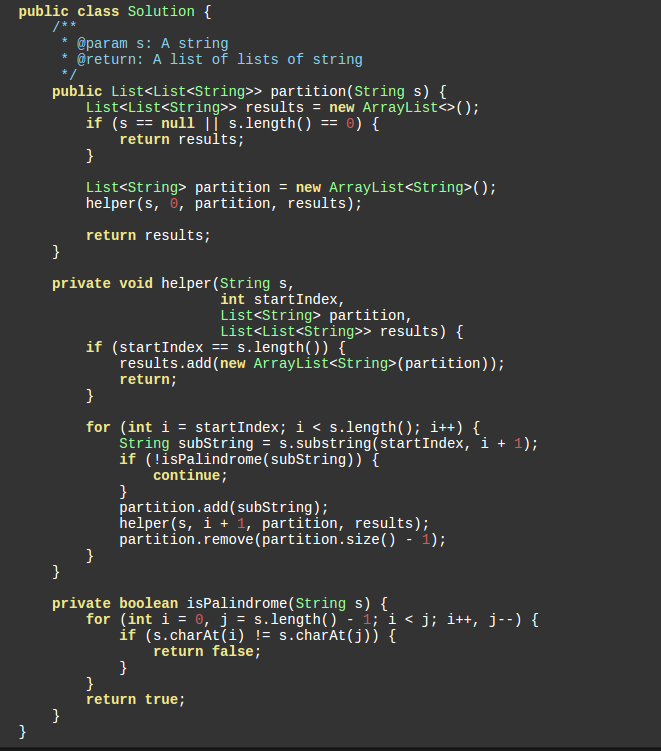
因为搜索是一种尝试, 是把以这个方案开头的所有都找到.
找完之后, 还要回到原来的状态, 要记得remove
Given a list of numbers, return all possible permutations.
问题模型:求出所有满足条件的“排列”。
判断条件:组合中的元素是顺序“相关”的。
时间复杂度:与 n! 相关。
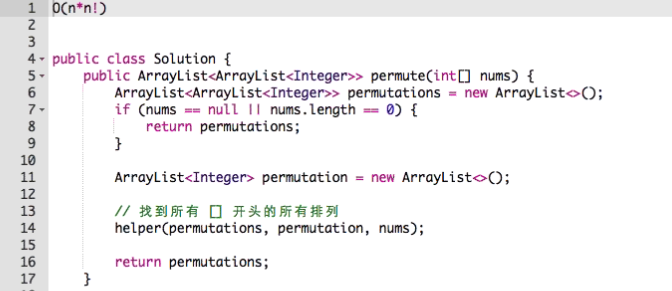

此题的时间复杂度是: O(n! * n)
和subsets的关系是:
permutation是可以回头取的, 但是不能重复取, 所以没有startIndex.
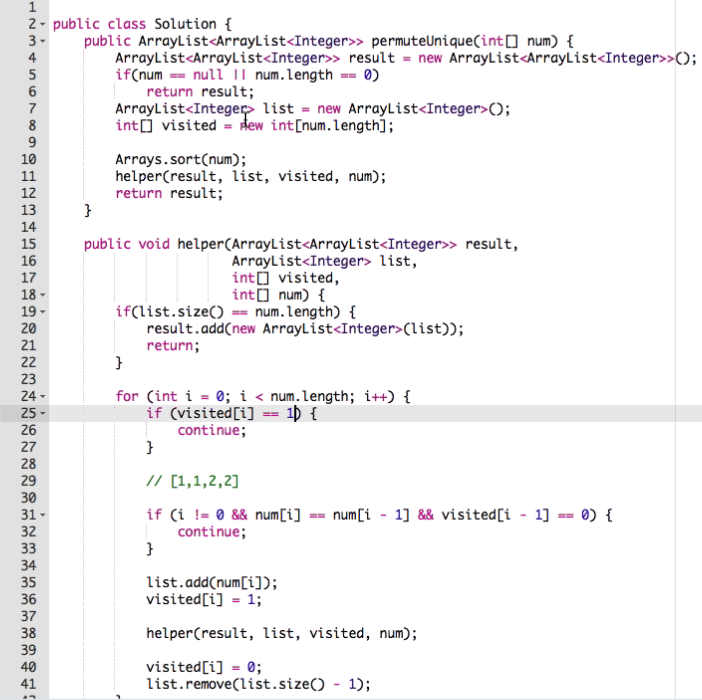
Given a list of numbers with duplicate number in it. Find all unique permutations.
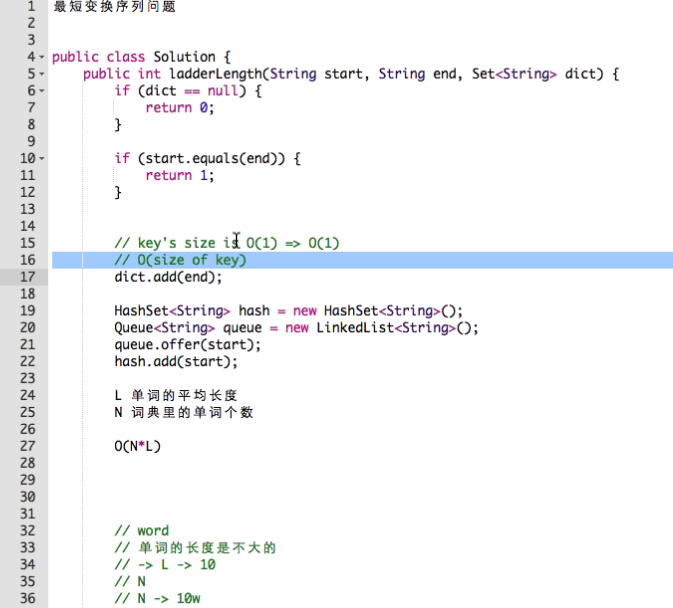
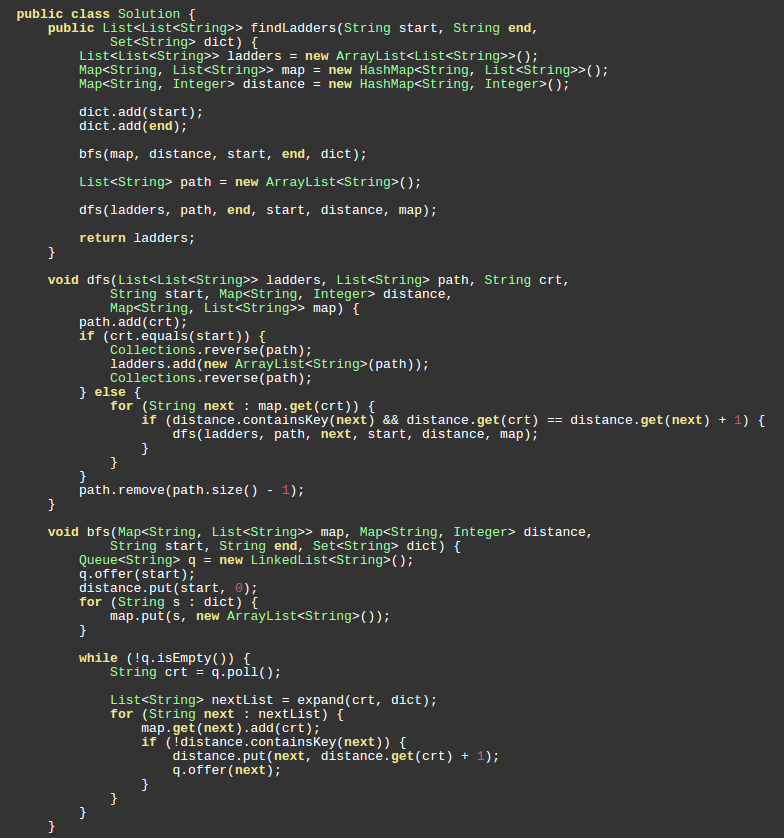
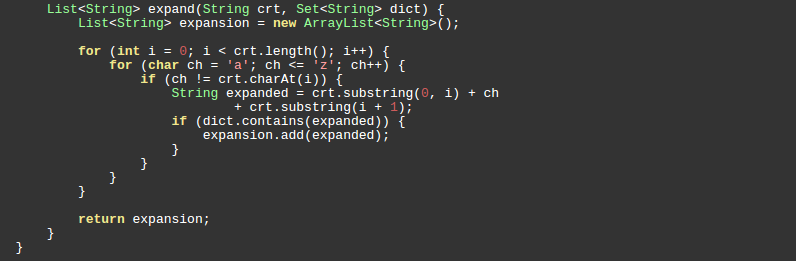
Given two words (start and end), and a dictionary, find the length of shortest transformation sequence from start to end, such that:
Only one letter can be changed at a time
Each intermediate word must exist in the dictionary
搜索的时间复杂度:O(答案总数 * 构造每个答案的时间)
举例:Subsets问题,求所有的子集。子集个数一共 2^n,每个集合的平均长度是 O(n) 的,所以时间复杂度为 O(n * 2^n),同理 Permutations 问题的时间复杂度为:O(n * n!)
动态规划的时间复杂度:O(状态总数 * 计算每个状态的时间复杂度)
举例:triangle,数字三角形的最短路径,状态总数约 O(n^2) 个,计算每个状态的时间复杂度为 O(1)——就是求一下 min。所以总的时间复杂度为 O(n^2)
用分治法解决二叉树问题的时间复杂度:O(二叉树节点个数 * 每个节点的计算时间)
举例:二叉树最大深度。二叉树节点个数为 N,每个节点上的计算时间为 O(1)。总的时间复杂度为 O(N)

public class Solution {
public int ladderLength(String start, String end, Set dict) {
if (dict == null) {
return 0;
}
if (start.equals(end)) {
return 1;
}
dict.add(start);
dict.add(end);
HashSet hash = new HashSet();
Queue queue = new LinkedList();
queue.offer(start);
hash.add(start);
int length = 1;
while(!queue.isEmpty()) {
length++;
int size = queue.size();
for (int i = 0; i < size; i++) {
String word = queue.poll();
for (String nextWord: getNextWords(word, dict)) {
if (hash.contains(nextWord)) {
continue;
}
if (nextWord.equals(end)) {
return length;
}
hash.add(nextWord);
queue.offer(nextWord);
}
}
}
return 0;
}
// replace character of a string at given index to a given character
// return a new string
private String replace(String s, int index, char c) {
char[] chars = s.toCharArray();
chars[index] = c;
return new String(chars);
}
// get connections with given word.
// for example, given word = ‘hot‘, dict = {‘hot‘, ‘hit‘, ‘hog‘}
// it will return [‘hit‘, ‘hog‘]
private ArrayList getNextWords(String word, Set dict) {
ArrayList nextWords = new ArrayList();
for (char c = ‘a‘; c <= ‘z‘; c++) {
for (int i = 0; i < word.length(); i++) {
if (c == word.charAt(i)) {
continue;
}
String nextWord = replace(word, i, c);
if (dict.contains(nextWord)) {
nextWords.add(nextWord);
}
}
}
return nextWords;
}
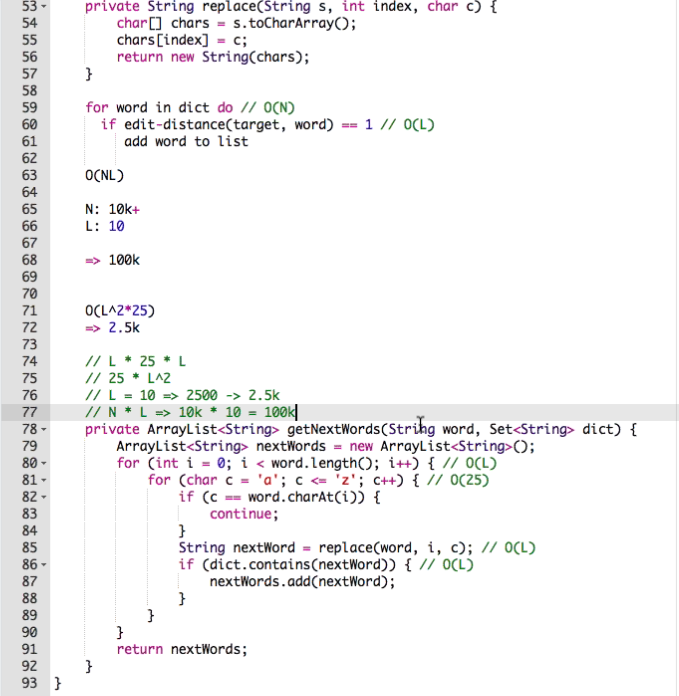
}L单词长度远小于N词典里的单词数, 所以
L: 10 N:10K
可以把时间从100k变成2.5k
ps: hash_map的时间是O(key.size())
因为key变成hash code即为index
Given two words (start and end), and a dictionary, find all shortest transformation sequence(s) from start to end, such that:
Only one letter can be changed at a time
Each intermediate word must exist in the dictionary
BFS+DFS

往B走, 没走的更近;
C才是正确的路线.
end ->start DFS
再reverse
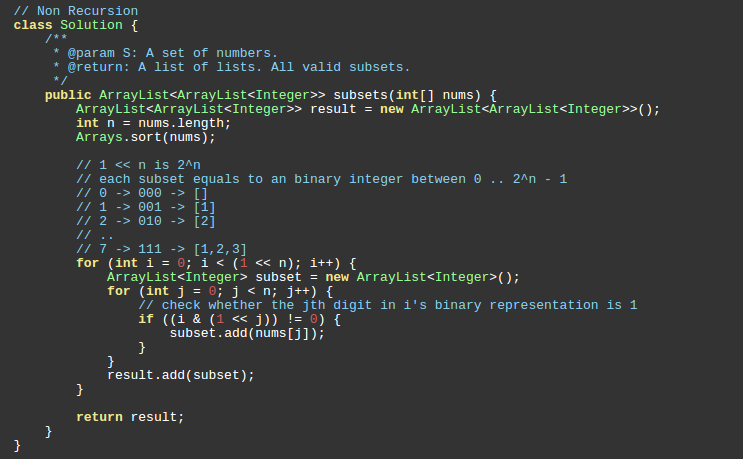
非递归和其他组合题不一样, 用位操作构造一个0~2^(n-1)的大循环
Given a list of integers, which denote a permutation.
Find the next permutation in ascending order.
Notice
The list may contains duplicate integers.
1 5 2 4 3找这些数字组成的稍微大那么一点的数
从右往左找第一个降序的地方, 把它和右边比他大的最小的换, 换完reverse回来
1 5 3 4 2
1 5 3 2 4
九章算法笔记 5.深度优先搜索 Depth First Search
原文:https://www.cnblogs.com/jiuzhangsuanfa/p/9895657.html