LeetCode：旋转图像【48】

题目描述

给定一个 n × n 的二维矩阵表示一个图像。

将图像顺时针旋转 90 度。

说明：

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。

示例 1:

给定 matrix = 
[
  [1,2,3],
  [4,5,6],
  [7,8,9]
],

原地旋转输入矩阵，使其变为:
[
  [7,4,1],
  [8,5,2],
  [9,6,3]
]

示例 2:

给定 matrix =
[
  [ 5, 1, 9,11],
  [ 2, 4, 8,10],
  [13, 3, 6, 7],
  [15,14,12,16]
], 

原地旋转输入矩阵，使其变为:
[
  [15,13, 2, 5],
  [14, 3, 4, 1],
  [12, 6, 8, 9],
  [16, 7,10,11]
]

题目分析

　　最笨的方法是模拟，可是在短时间内根本无法准确提取出模拟的所有边界判断条件，代码异常冗余，且无法进行优化。

　　然后怎么办呢？我们分析题目可以看出一个隐含条件，就是所给的矩阵一定是正方形的。因为我们不能新建数组，那么原有数组为长方形的话，无论如何我们都是无法表示结果的。

　　到这里然后呢？我们首先将其进行行列转置！

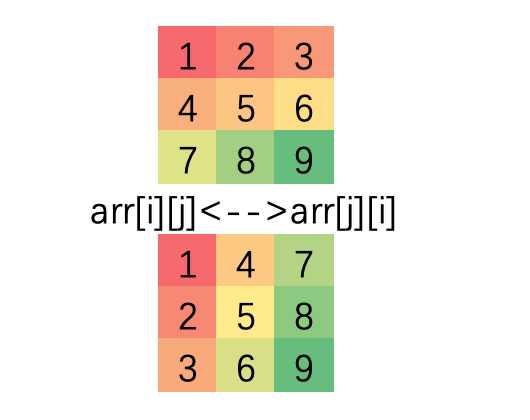
　　接着，我们再关于中心轴做镜像变换，swap(arr[i][j], arr[i][matrix.length-1-j])

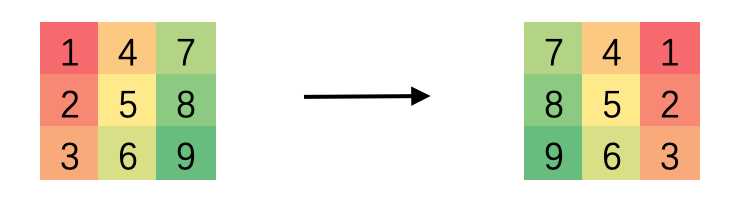
　　最后我们应该思考一下为什么这样可以呢？

Java题解

    public void rotate(int[][] matrix) {
        for(int i = 0;i<matrix.length;i++) {
            for (int j = i; j < matrix[0].length; j++) {
                int temp = 0;
                temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        for(int i =0 ; i<matrix.length; i++){
            for(int j = 0; j<matrix.length/2; j++){
                int temp = 0;
                temp = matrix[i][j];
                matrix[i][j] = matrix[i][matrix.length-1-j];
                matrix[i][matrix.length-1-j] = temp;
            }
        }
    }

LeetCode：旋转图像【48】

原文：https://www.cnblogs.com/MrSaver/p/9897148.html