故事出真知
阿珍 爱上了 阿强
但 被他们的父母 拒绝 了
没错 狗血的近亲结婚剧情开始了
阿珍 说:
不行,我深深爱着我的阿强,谁也不能把我们分开
阿强 深情地望着阿珍 说
一定会有机会的!
此时 他突然灵机一现
只要不是 三代近亲 就可以了!!!
现在 深深相爱的阿珍和阿强 将他们的命运托付给你
没错需要身为爷爷的你帮助他们寻找共同的祖宗
只要是 三代以外 他们明天就成婚
否则会 一起私奔
如图
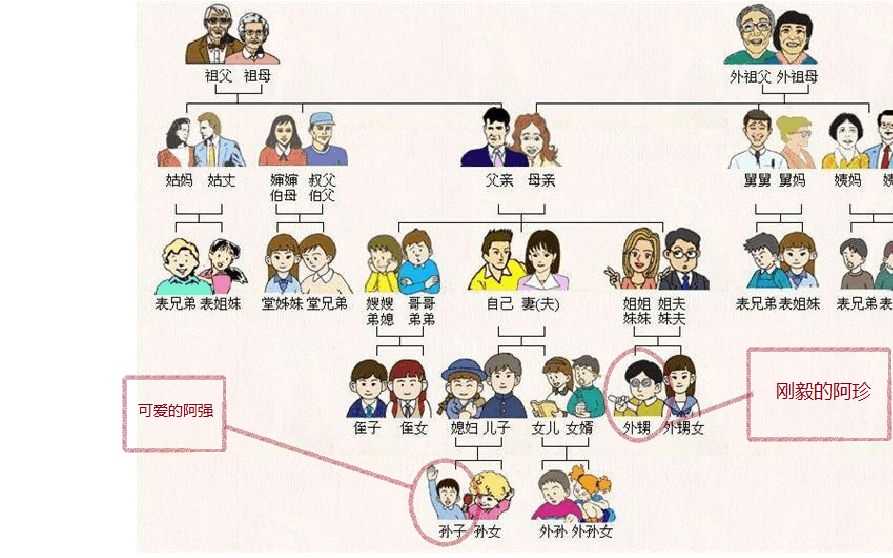
没错 你用眼看就可以看出来 他们的最近的祖宗 是你爸和你妈
不过你是怎么看的呢
不错 往上看 不停地往上看 直到他们的祖宗是同一个人
看
阿强他爸是你儿子 阿珍他妈是你妹妹
阿强他爸的爸爸是你 阿珍他妈的爸爸是你爸爸
阿强他爸的爸爸的爸爸是你爸爸
啊 没想到最近的祖宗这么近 我的阿强啊!
故事就到这里
哈 是不是感觉这关系有点拗口,不过没关系,这才刚刚开始
从故事中 你可以大概了解 寻找最近公共祖先的方式
就是 从两个人物 即阿珍与阿强开始 往上找 直到祖宗相同为止
巧了 LCA算法的主体思路就是这样的 哈哈你可以光荣地说那鼎鼎大名的LCA抄袭你伟大的思想了
别嘚瑟 你能实现么,而且这才刚刚开始
从 实现方式我们可以知道
一是我们要建立一套完整的关系图 否则谁谁 你都不认识
二是从关系图中明确辈数关系 就是 你爸是谁 你儿子是谁
所以
构造关系图 需要用 前向星 (方便,快捷) 至于树就太麻烦了
struct Edge{ int nex,to; //nex:这条边的起点 to:边的终点 }; Edge edge[31]; int head[31],node[31],cnt=0; //head数组保存边的序号 void add(int a,int b) //加边 { cnt++; edge[cnt].to=b; edge[cnt].nex=head[a]; head[a]=cnt; }
这样一来就有一个大概关系,但你现在只知道你爸和你儿子,却不知道你爷爷是谁
所以 我们需要利用 搜索 来疏通关系
void dfs(int u,int fa) //u为当前节点 fa为它父亲节点 { d[u]=d[fa]+1; //u比fa年轻一辈 for(int i=head[u];i!=-1;i=e[i].next) //找它的儿子 { int v=e[i].v; if(v!=fa) // 不是爸爸,就是儿子 dfs(v,u);//叫一声爸 } }
其中 d 数组 即 deep 表示深度,也就是辈数
因为 树结构的特殊性
如果有n个节点 必须有n-1条边
除了叶子节点和根节点外 每个节点都有两条与它相连的边
你可以这样理解 你爷爷生了你爸,你爸生了你,而你至今单身
利用树的特殊性 与 前向星完美结合 就可以疏通一切关系
现在可谓是 万事俱备 只欠东风
最近的老祖宗你们好吗!
int lca(int a,int b) //不带任何优化的lca查找 { if(d[a]>d[b]) swap(a,b); //保证a是在b结点上方,即a的深度小于b的深度 if(a==b) return a; //特判,如果b上来和就和a一样了,那就可以直接返回答案int mark[31],ans=1; int u=a; //记录当前节点 阿珍 for(int i=head[u];i;i=edge[i].nex) { int v=edge[i].to; if(d[v]<d[u]) //如果它是你爸爸 { u=v;mark[ans++]=v; //把你换成爸爸,找你爸爸的爸爸, 同时标记一下 continue; } } u=b; //阿强 for(int i=head[u];i;i=edge[i].nex) { int v=edge[i].to; if(d[v]<d[u]) // { for(int i=1;i<=ans;i++) if(v==mark[i]) {cout<<"找到了!!";return;} //看看 你现在的祖先 在对方的祖先中有没有 如果是就成功了 否则继续 } } }
如此一来大功告成,只可惜阿珍与阿强只能去私奔了
所以你以为 这就是LCA?不,这才刚刚开始
最后求lca的过程用了 dfs加比较 时间复杂度与边的数量成正比 即O(2*E)
有没有什么更快的优化呢 不错魔性 倍增
预知后事如何 请代下回分解
原文:https://www.cnblogs.com/turn-wind/p/9898817.html