希尔排序,又称“缩小增量排序”,通过将原始列表分成若干个子列表来改进插入排序,每个子列表使用插入排序。
如何选择子列表的形式是希尔排序的关键。希尔排序使用增量i(有时又成为间隙gap)来创建子列表,而不是将原始列表连续的切分。这种方式可以将相隔较远,较为分散的元素通过增量划分到一组,改进了一次插入排序只能在相邻间元素进行比较。
如下图所示,我们有9个元素,如果我们使用增量3,则可以将原始列表分成3个子列表,每个子列表3个元素。子列表为{a1, a4, a7},{a2, a5, a8},{a3, a6, a9}。然后分别对这3个子列表使用插入排序。
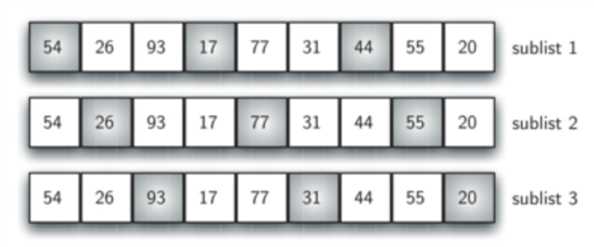
分别进行完一次插入排序后,结果如下图。虽然这个列表没有完全排序,但发生了一些非常有趣的事情。 通过对子列表进行排序,我们将这些元素移动到更接近实际所属的位置。
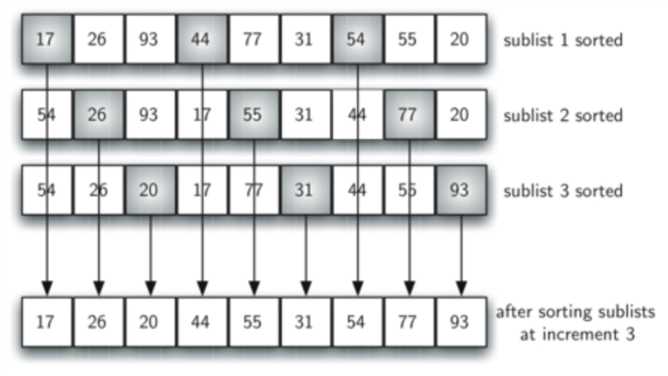
由上图可以看出,通过增量3,分别对3个子列表进行排序后,我们得到一个接近完全排序的列表。只有20,31,54三个元素没有得到排序,而其他元素的相对位置已经保持排序。
这次我们将增量i变为1,则此时子列表和上图中的列表相同,然后对其运用插入排序。则最终结果如下图。
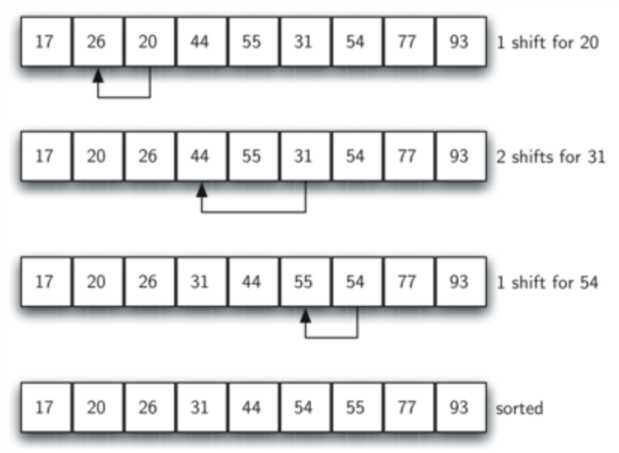
一般情况下,我们会这样选择增量:假设列表长度为N,则一次使用N/2,N/4,......,1。下图为另一种增量的使用方式:N为9,则第一个增量为4。
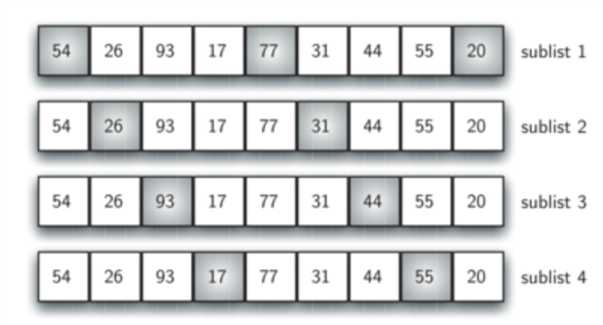
def shell_sort(a_list):
sublist_count = len(a_list) // 2
while sublist_count > 0:
for start_position in range(sublist_count):
gap_insertion_sort(a_list, start_position, sublist_count)
print("After increments of size", sublist_count, "The list is", a_list)
sublist_count = sublist_count // 2
def gap_insertion_sort(a_list, start, gap):
for i in range(start + gap, len(a_list), gap):
current_value = a_list[i]
position = i
while position >= gap and a_list[position - gap] > current_value:
a_list[position] = a_list[position - gap]
position = position - gap
a_list[position] = current_value整个算法的实现逻辑如下:shell_sort方法为主方法,首先获取增量sublist_count用以划分子列表。每划分一次,就使用gap_insertion_sort对各个子列表进行插入排序,直至增量值变为1。值得注意的是,在gap_insertion_sort中,实现的依然是上一讲中的插入排序,只不过我们多子列表进行插入排序。在一次插入排序算法中,我们遍历的是整个列表,在子列表插入排序中,我们每间隔一个gap进行遍历。
乍一看,你可能认为shell排序不能比插入排序更好,因为它在最后一步执行完整的插入排序。 然而,事实证明,这个最终插入排序不需要进行很多比较(或移位),因为列表已经被先前的增量插入排序预先排序,如上所述。换句话说,每次子列表插入排序产生一个比前一个更“排序”的列表。 这使得最后的插入排序非常迅速。
对一般的shell sort进行分析超出了本文的范畴。但我们可以说,根据上面的描述,shell sort的时间复杂度通常介于\(O(n)\)和\(O(n^2)\)之间。通过改变增量,如使用\(2^k-1\)(1,3,7,15,31,......),可以将时间复杂度变为\(O(n^\frac{3}{2})\)。
一次插入排序是稳定的,但希尔排序确实不稳定的。
原文:https://www.cnblogs.com/jeffrey-yang/p/9901561.html