洛谷P4994 终于结束的起点

题目背景

终于结束的起点
终于写下句点
终于我们告别
终于我们又回到原点
……

一个个 OIer 的竞赛生涯总是从一场 NOIp 开始，大多也在一场 NOIp 中结束，好似一次次轮回在不断上演。
如果这次 NOIp 是你的起点，那么祝你的 OI 生涯如同夏花般绚烂。
如果这次 NOIp 是你的终点，那么祝你的 OI 回忆宛若繁星般璀璨。
也许这是你最后一次在洛谷上打比赛，也许不是。
不过，无论如何，祝你在一周后的比赛里，好运。

当然，这道题也和轮回有关系。

题目描述

广为人知的斐波拉契数列fib(n) 是这么计算的

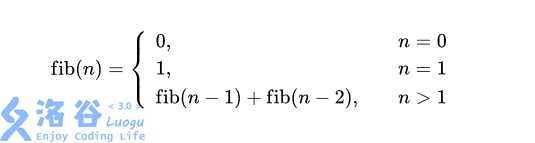
也就是 0,1,1,2,3,5,8,13?，每一项都是前两项之和。

小 F 发现，如果把斐波拉契数列的每一项对任意大于 11 的正整数 MM 取模的时候，数列都会产生循环。

当然，小 F 很快就明白了，因为 (fib(n−1)modM) 和 (fib(n−2)modM) 最多只有 M2 种取值，所以在 M2 次计算后一定出现过循环。

甚至更一般地，我们可以证明，无论取什么模数 MM，最终模 MM 下的斐波拉契数列都会是 0,1,?,0,1,?。

现在，给你一个模数 M，请你求出最小的 n>0，使得 fib(n)modM=0,fib(n+1)modM=1。

输入输出格式

输入格式：

输入一行一个正整数 M。

输出格式：

输出一行一个正整数 n。

输入输出样例

2

3

6

24

说明

样例 1 解释

斐波拉契数列为 0,1,1,2,3,5,8,13,21,34,?，在对 22 取模后结果为 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, \cdots0,1,1,0,1,1,0,1,1,0,?。

我们可以发现，当 n=3 时，f(n)mod2=0,f(n+1)mod2=1，也就是我们要求的 n 的最小值。

数据范围

对于 30% 的数据，M≤18；

对于 70% 的数据，M≤2018；

对于 100% 的数据，2≤M≤706150=0xAC666。

提示

如果你还不知道什么是取模 (mod)，那我也很乐意告诉你，模运算是求整数除法得到的余数，也就是竖式除法最终「除不尽」的部分，也即amodM=k?a=bM+k (M>0,0≤k<M)其中 a,b,k 都是非负整数。

如果你使用 C / C++，你可以使用 % 来进行模运算。

如果你使用 Pascal，你可以使用 mod 来进行模运算。

/*
    这到底是起点还是终点呢？
    这道题很简单，暴力就可以水过，甚至不要打表啥的
    滚动地使用a,b,c三个变量，a是第一个数，b是第二个数，c是第三个数
    其他的看程序就好 很容易理解的
*/

#include <bits/stdc++.h>

using namespace std;

int a,b,c,ans;

int main(){
    int mod;scanf("%d",&mod);
    a = 0,b = 1;
    while(true){
        ans++;
        c = (a+b)%mod;
        if(c == 1 && b == 0){
            printf("%d\n",ans);
            return 0;
        }
        a = b%mod;
        b = c%mod;
    }
    return 0;
}

洛谷P4994 终于结束的起点

原文：https://www.cnblogs.com/bryce02/p/9909234.html