昨天刷这样一道编程题:
--------------------------------------------------------------------------------------------------
求连续子数组的最大和。
--------------------------------------------------------------------------------------------------
看到题目后,我的第一反应:“可以根据积分原理来解决,先将数组从左到右进行累加,根据累加数组的最小值、最大值来计算连续子数组的最大和”。
想象中,累加数组的折线图大约是这个样子:
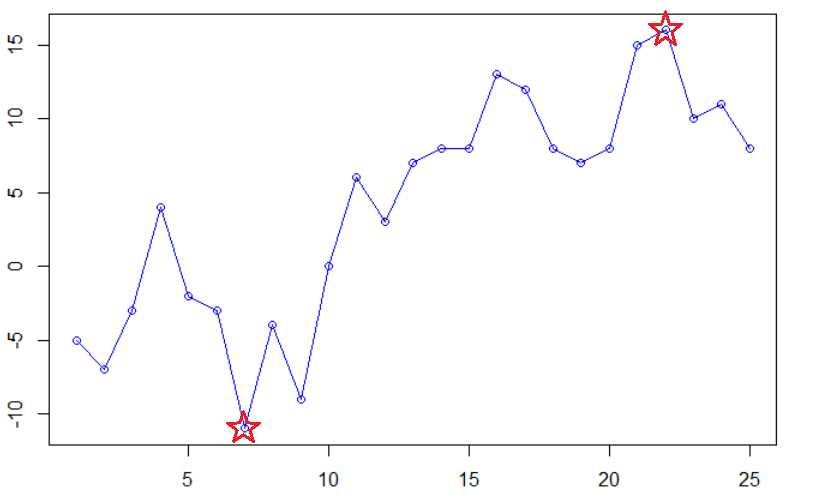
“很显然,连续子数组和的最大值为:累加数组的最大值与最小值之差。”
“如果累加数组的全局最大值在最小值左边怎么办?”
“那就找它的局部最大值、最小值,再比较多个局部的结果,取最大值。”
“如何找局部最大值、最小值?”
“把累加数组切分为两部分,迭代计算。”
头脑里这么想着,手指头也跟着活动起来了,反正这就和“累加数组”杠上了。
写完后提交代码试运行,部分case不通过。然后修修补补,终于提交通过了。
代码如下:
def find_max_sublist_sum(a_list):
# 空list直接返回结果0
if len(a_list) == 0:
return 0
# 去除list前面连续的负整数,生成新的new_list;如果list全部元素为负,则返回结果0
indx = 0
for x in a_list:
if x > 0:
break
else:
indx += 1
if indx < len(a_list):
new_list = a_list[indx:]
else:
return 0
# 从前往后,计算new_list元素的累积和,生成accumulate_list
accumulate = 0
accumulate_list = []
for x in new_list:
accumulate += x
accumulate_list.append(accumulate)
# 找出累积和列表最大值、最小值对应的index
index_min = accumulate_list.index(min(accumulate_list))
index_max = accumulate_list.index(max(accumulate_list))
# 根据累积和列表的最大值、最小值位置进行分类计算
if index_min < index_max: # 最小值在最大值左边,取最小值到最大值区间内增量
return max(accumulate_list) - min(min(accumulate_list), 0)
elif index_min == index_max == 0: # 最小值、最大值均 index == 1,说明列表只有一个正数
return accumulate_list[0]
else: # 将列表分成2部分,递归处理
list1 = new_list[:index_max+1]
list2 = new_list[index_max+1:]
return max(find_max_sublist_sum(list1), find_max_sublist_sum(list2))
if __name__ == ‘__main__‘:
import sys
for line in sys.stdin:
testlist = line.split(‘,‘)
testlist = [int(testlist[i]) for i in range(len(testlist))]
print(find_max_sublist_sum(testlist))
自我感觉,这个解法有些复杂,但是也没认真去想其他的办法。
今天再回过来看时,看到@牛客692333551号贴出来的解法,我恍然大悟。
@牛客692333551号解法如下:
x = [int(i) for i in input().split(‘,‘)]
res = 0
d = max(0, x[0])
res = max(res, d)
for i in range(1, len(x)):
d = max(d + x[i], 0)
res = max(res, d)
print(res)
原来自己的方法太蠢、太丑了!不忍直视!
为什么自己如此坚决地捍卫自己的“第一反应”,宁可绞尽脑汁去修修补补,也不愿去换个思路去想?
第一反应是自己的直觉,直觉一般凭借经验做出反应,却不一定靠谱,特别是那些经验不足者的直觉。
对于弹出的直觉反应,我们应该用理性思维去进行判断。
我们不要太懒惰了,任由着直觉去乱来,最后还得去帮它填坑。
参考:
https://www.nowcoder.com/questionTerminal/459bd355da1549fa8a49e350bf3df484
原文:https://www.cnblogs.com/zhangwei22/p/9931645.html