算法第3章作业
一、 你对动态规划算法的理解。
动态规划适用于最优解的问题。动态规划的基本思想是将待求问题分成若干个子问题,先求子问题,再从子问题的解得到原问题的解,它的子问题的解往往不是相互独立的。为避免大量的重复计算,动态规划会用一个表来记录已解决的子问题的答案。
二、 分别列出编程题1、2的递归方程。
编程题1:
for(int i=2;i<=n;i++){
b[i]=1;
for(int j=1;j<=i;j++){
if((a[i]>a[j])&&(b[j]>=b[i]))
b[i]=b[j]+1;
}
if(max<b[i]) max=b[i];
}
编程题2:
for(int i=n-1;i>0;i--) {
for(int j=i+1;j<=n;j++) {
if(j-i==1) a[i][j]=a[i][j];
else{
int temp;
for(int k=i+1;k<=j;k++) {
min=a[i][k]+a[k][j];
if(a[i][j]>min) {
a[i][j]=min;
}}}}}
三、 说明结对编程情况。
本章动态规划我主要偏向于自我完成多一点,因为这一章确实比较难懂,需要借助书本上的知识和上网查阅。判断选择题不是很会做,经过翻书、上网和问同学与他们一起讨论,最终还是有点糊里糊涂的,不是很能理解。其中编程题2:租用游艇问题,对于填充数据,我还向谢思婷同学请教了循环填充数据的方式,首先分析了i<k<j,由此得图:
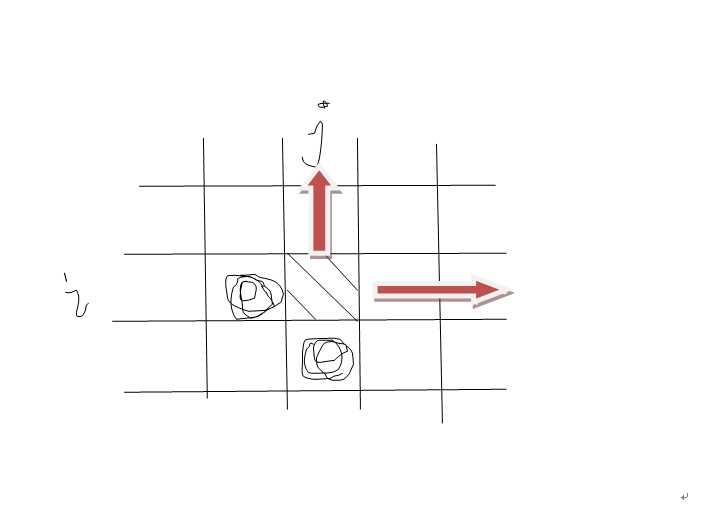
首先我们分析了以上图方法填表的方式,i是自下而上,就是从n-1到1;j是左左向右填表,即从i+1到n;对于k来说,就是比i大比j小,即从i+1到j;从而得出三个循环条件。此后,我们还强调了一种特殊情况,就是从第一站到第二站的时候,直接就等于本身。
原文:https://www.cnblogs.com/zmzmkkk-/p/9940481.html