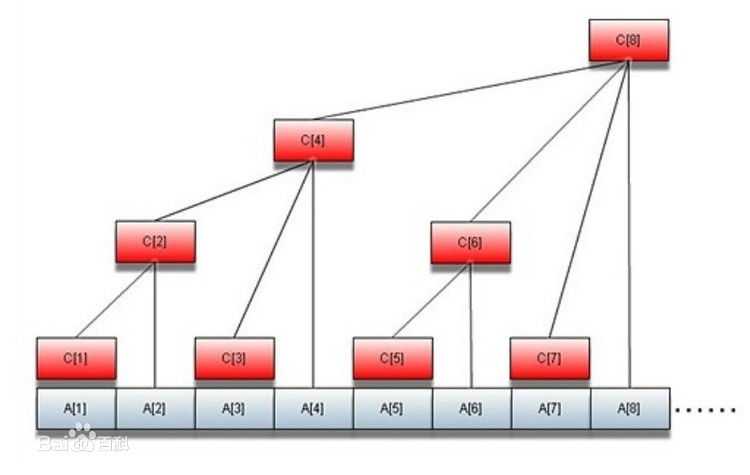
(建议边对着图边看解释)
背景:若在线地修改数列里某个数的值,其维护【前缀和】的复杂度太高
树状数组c性质:
1、c[i]的管辖区间以a[i]结尾,从某种意义来说,c[i]与a[i]一一对应
2、c[i]的管辖区间长2^k,k是i的二进制末尾0的个数
3、父亲的管辖区间是儿子区间长度的二倍
4、c[i]的值是a的和,c[i]=a[i-2^k+1]+……+a[i]
主要操作解释:
1、修改某个元素并一路往上更新
修改a[i],从第一个元素c[i]开始(c[i]一定以a[i]结尾),每次下标i加上其管辖区间长度2^k即得到父亲的下标,也就是父亲管辖区间的最后一个元素下标
1 //返回2^k 2 static int lowbit(int i){ 3 return i&(-i); 4 } 5 6 static void update(int i,int x){ 7 while (i<=n){ 8 c[i]+=x; 9 i+=lowbit(i); 10 } 11 }
2、求a中前i项的和
累加i前的所有最大子树的根的值,(每次减小i的2^k的值即可从一颗最大子树的根直接跳到另一颗最大子树的根)
1 static int query(int i){ 2 int sum=0; 3 while (i>0){ 4 sum+=c[i]; 5 i-=lowbit(i); 6 } 7 return sum; 8 }
原文:https://www.cnblogs.com/towerbird/p/9941030.html