NOIP2018 完跪……滚回学校考半期 QwQ
这篇不是题解 awa ,题解之后会发布的,毕竟我还没有AC呢
又及……G2020 陌路笙歌 - 再见(╯▽╰)
第一次考提高组,之前和将要AFO的G2020一起培训了很久,感触颇深~毕竟距离AFO就只剩两年了,还是抓紧吧
星期五试机的时候有一点爆炸……O(nlogn) 的最长上升子序列都写挂了。
考试的时候根据策略先扫了一遍所有的题——嗯~好!没几道会做的 QwQ
一群人说AK Day1……然后高中那边说只有3个人没AK,然而真的很爆炸
一开始的奇葩思路:找到最小值,作为分隔点分治;
怎么找最小点呢?线段树!-_-|||
然后发现好像很难实现……如果区间里有多个最小值怎么办?
又一想,NOIP day1 t1 线段树??? Impossible!
再看一眼……贪心!尽可能多填(似乎是很明显的)!单调栈!(终于对了)
嗯,用了1h做出来
好熟悉的题目……完全背包!(正解是这样)
然后莫名递推式写挂,多写了一个 O(n)
出题人非常友好~特殊数据挺多。
先说我自己的做法吧……因为时间不够,就没有写正解,直接骗分:
当m=1时直接跑DFS,加一个最优性剪枝;
当i和i+1相邻时,就相当于是一个链,所以可以二分答案,贪心检测(即从链的端点出发,尽可能选线段,记录现在的线段总长为tot,当tot>mid即符合条件时,就可以清零tot,找到的路径条数+1)
其实想到二分+贪心判断就已经接近正解了,还是有一点可惜。据说正解先二分答案,然后从叶子节点出发尽可能取线段(边),当达到mid时就形成了一条新的路径;当两个路径会于同一个节点,即LCA,则判断两条路径相连能否>=mid,可以就形成新路径,否则取较长的路径连接根节点再往上推。
听说很水,但是还是挂了;似乎是230的分。
好像有一点Difficult,对于一个初中生真是太不友好了(似乎对于zjx和tly巨佬来说不是这样的……)
比较简单的贪心;
从1出发;
对于树形结构先走较小点;
然后又一个环的情况挂了……时间复杂度没分析对,本来 O(n^2)能过,但是就没写,以为会 TLE;
看题目的时候第一眼——结论题!!!
然后第一题放弃后就开始死推结论,然后推出来一个似乎是正确的结论——
如果A,B两个位置,A在B的右上方,则A的填的数字不能大于B;
验证了一下2*2的情况,是对的(开心);然后手算3*3……为什么我算出来是144?!
心态就崩了……最后只好将6*6的所有答案通过DFS打表跑出来(效果不错)
然后赛后发现很多同学和我的结论一样……都卡住了,于是我们开始讨论——我把我有点疑惑的一点画出了图:
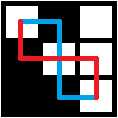
上面黑色块填的数字是1,看得出来蓝色路径为 "RDDDR",红色路径为"DRRRD",但是蓝色路径经过的点为"01010",红色路径经过的点为"01000"……
尴尬……结论完全错误
第一眼树形DP(开心)
然后发现多组询问,沉思QwQ
想不出来,就只好写 O(n,m) 的,也就是对于每一次询问都做一次 O(n) 的DP
but……树形DP写挂了啊——因为如果当前点是询问中要求必须选/不选的点,dp状态中的一个值就需要赋值为INF,但是我把这一步操作放在了访问当前节点的儿子时处理的……也就是说如果当前节点是被限制的一个节点,在访问它的一个合法儿子(不是父亲)时,我就把某一个dp状态设为INF(比如当点u不能选时,表示“选择u点”的状态就是INF)。但是会出现一个问题——限制叶子节点时,因为叶子节点没有子节点,所以它的不合法状态就不会标记为INF,就挂了。
关键是只要存在一个这样的询问,整个数据就会挂掉QwQ
唉,以前常喜欢说 “路还很长,要慢慢走” ,但现在看来路虽长,但时间却不多了啊!
已经初三了,下一年就是高一,再过两年,没进省队就要AFO了(虽然不是真正的OIer,但是还是不愿提到AFO这个终会到来的事实)
后面的路得加紧走了(我设立了一个计划,刷《挑战程序设计竞赛》的习题,尽可能每周6道)
希望大家能共同进步(膜谁也没用,考场上还是孤单一人)
原文:https://www.cnblogs.com/LuckyGlass-blog/p/9946014.html