解决大部分字符串问题的大杀器
给一下clj课件:戳我
字符串常见问题:各种匹配
1.LCP
2.子串匹配
3.模式串和主串匹配
4.回文串?也算匹配吧。。。
经典例子:
给两个串,求最长公共子串长度。
用hash表可以做到nlogn
后缀自动机可以做到O(n)
我们需要一个可以识别某个串是否为某个主串的子串、处理主串的子串信息、串和串之间进行匹配的问题。
朴素的做法是,对每个子串建立一个节点,然后连边,O(n^2)
考虑的优化是,发现一些子串会出现很多次,一些子串出现所有的出现位置的集合是同一个集合!
对这个进行优化
对于某个串s,所有出现的位置的集合是:{r1,r2,...,rm}
那么,这个集合就是Right(s)
由于许多的串si,可能Right集合都是Right(s)
如果我们给定集合Right(t)
再给定属于这个集合的字符串的长度len
随便选择一个r,那么这个字符串就已经唯一确定了。
一个Right集合会包含若干个字符串
那么,其len的范围一定是一个区间[max,min]
那么,为了处理方便,我们会把这些串压缩在一起。
保留这个Right集合的max
我们就会定义Right(s)为一个“状态”
这个“状态”,包含了所有的可能匹配到的节点末尾的位置ri,以及可能已经匹配出来的字符串集合si
证明:
首先易证,一个字符串属于且仅属于一个Right集合。
设两个集合s1,s2相交,r是交集的某个元素
那么对于一个属于s1的字符串string1
一个属于s2的字符串string2
由于两个字符串都可以以r作为末尾出现一次,由于一个字符串属于且仅属于一个集合
所以,string1!=string2
不妨设len(string1)=l1<len(string2)=l2
那么,显然地,string2出现的位置,string1必然也会出现。
所以,s2中有的元素ri,s1中必然也有
并且,必然存在一个元素r0,满足s1中有,但是s2中没有(否则s1,s2其实是一个集合)
那么s2就是s1的真子集。
证毕。
发现,Right集合的两个性质非常给力。
真子集的包含关系可以看做父子关系
Right集合之间的不相交关系可以看做非祖宗关系。
图示:from clj
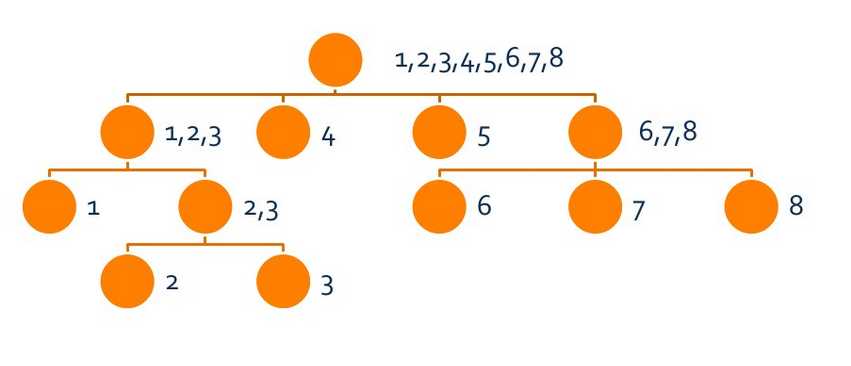
可以发现,对于集合字符串长度,有mx[fa[i]]+1=min[i]
进而可以这样理解:
father集合的结束位置更多,所以满足的字符串长度必然更短。
而且,有mx[fa[i]]+1=min[i]
叶子节点只有一个r
那么,如果从某个叶子节点往上找,那么所遍历的长度,就是以r结尾的所有子串。
数组:(节点及$Right$集合,即所谓的“状态”)
$fa[i]$——节点$parent$树上的$father$
$ch[i][∑]$——节点的出边(类比$trie$树),指向添加字符$x$后到达的下一个节点($s[ri+1]==x$的会继续匹配上,这些$ri$就构成了目标的节点。如果没有,那么就指向$NULL$(实际不会操作,即$0$号节点就是$NULL$节点))。$∑$是字符集大小
$len[i]$——某个节点的所有字符串中最长的长度。
$nd$——当前匹配的最后一个节点$p$。若当前是$L$,则$Right(p)={L}$
$cnt$——节点个数。
我令$rt$节点为$1$
开始$nd=rt$
增量法构造,即每次插入一个字符$x$。设当前已经插入的字符串长度是$L$
我们要做的,就是新加入这个节点之后,维护好所有的后缀(使得后缀都能走出来)。
需要维护$fa$指针,和$ch[∑]$指针。
(以下祖先指$parent$树上的祖先)
建立一个$np$节点,其实有$Right(np)={L+1}$
赋值:$len[np]=L+1$
对于$p$的祖先,$p_1,p_2,...p_k$
存在一段$p_1,p_2,...p_{v-1}$
满足都没有$ch[*][x]$的边(也即都指向$NULL$)
对于$p_v$存在一个指向$x$的边
设$q=ch[p_v][x]$,
存在两种情况
$I$
$len[q]==len[p_v]+1$
那么意味着,之前所有的状态$q$代表的位置都可以加一个$x$匹配上将要加入的字符
那么可以直接把$q$当做$np$的$father$
(这个时候,其实$q$的$Right$集合发生了变化,已经加入了一个位置$L+1$)
就可以结束这次插入。
$II$
$len[q]>len[p_v]+1$
这是什么意思?
图示:(第一个串有一个B错了)
那么意味着,$q$抛弃了一些$p_v$的存在位置,并且使得长度增加了。
那么,$q$一定抛弃了以$L$结尾的位置。
否则,会存在一个离p更近的祖先,满足存在指向$x$的边。
所以,这样的$q$匹配上$x$之后,一定不会包含$L+1$位置。
那么,这个$q$,一定不能作为$np$的$father$(因为不包含$L+1$这个位置)
所以,我们新建一个节点$nq$
这个$nq$的$Right$集合,其实是:$Right(q)∪\{L+1\}$
我们还要对$nq$进行一些处理。
$fa[nq]=fa[q]$
$fa[q]=nq$
$fa[np]=nq$
$len[nq]=len[p_v]+1$
对于$nq$,所有$q$的出边,都是$nq$的出边
对于$ch[p_i][x]==q$的$p$的祖先(一定是连续一段),把出边$ch[p_i][x]$都设置为$nq$
然后就可以结束了。
代码:
luoguP3804 【模板】后缀自动机
(注意,点数是2倍)
#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^‘0‘) using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch==‘-‘)&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=3e6+6; int n,m; ll ans; char s[N]; struct SAM{ int ch[N][30],cnt; int fa[N],nd;int sz[N]; int hd[N],tot; int len[N]; struct node{ int nxt,to; }e[2*N]; void init(){nd=1;cnt=1;} void add(int x,int y){ e[++tot].nxt=hd[x]; e[tot].to=y; hd[x]=tot; } void ins(int c,int pos){ int p=nd;sz[nd=++cnt]=1; len[nd]=pos; for(;p&&ch[p][c]==0;p=fa[p]) ch[p][c]=nd; if(p==0) {fa[nd]=1;return;} int q=ch[p][c]; if(len[q]==len[p]+1){fa[nd]=q;return;} len[++cnt]=len[p]+1; for(reg i=1;i<=26;++i) ch[cnt][i]=ch[q][i]; fa[cnt]=fa[q];fa[q]=cnt;fa[nd]=cnt; for(;p&&ch[p][c]==q;p=fa[p]) ch[p][c]=cnt; } void build(){ for(reg i=2;i<=cnt;++i) add(fa[i],i); } void dfs(int x){ for(reg i=hd[x];i;i=e[i].nxt){ dfs(e[i].to);sz[x]+=sz[e[i].to]; } if(sz[x]!=1) ans=max(ans,(ll)sz[x]*len[x]); } }sam; int main(){ scanf("%s",s+1); n=strlen(s+1);sam.init(); for(reg i=1;i<=n;++i) sam.ins(s[i]-‘a‘+1,i); sam.build();sam.dfs(1); printf("%lld",ans);return 0; } } int main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/11/16 21:54:31 */
维护了所有的后缀,所以维护了所有的子串。
并且Parent指针类似于AC自动机的fail指针,转到了可能可以继续匹配的某个出现过的、更短的字符串。
跳一次Parent,匹配长度至少-1
所以,能失配后,快速利用保留信息,所以也可以支持匹配。
SP1811 LCS - Longest Common Substring
2.
原文:https://www.cnblogs.com/Miracevin/p/9974743.html