堪称明明看得见,就是写不出的一类恶心题。
通常细节颇多。
一旦方法选择合适,代码量和效率都会提升不少。
推荐:
(以下图片均来自此博客)

struct po{ double x,y; po(){} po(double xx,double yy){ x=xx;y=yy; } po friend operator +(po a,po b){ return po(a.x+b.x,a.y+b.y); } po friend operator -(po a,po b){ return po(a.x-b.x,a.y-b.y); } };
(加减为了向量方便赋值)

double dis(po a,po b){ return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); }
(x=(x1+x2)/2,y=(y1+y2)/2)

struct vec{ double x,y; vec(){} vec(po a){ x=a.x,y=a.y; } double len(){ return sqrt(x*x+y*y); } };
向量加减和数乘略了。
len是向量的模长。

double dot(vec a,vec b){ return a.x*b.x+a.y*b.y; }
点积用处:可以通过两个向量的点积正负,判断向量夹角是锐角、直角、钝角

double cross(vec a,vec b){ return a.x*b.y-a.y*b.x; }
意义,两个向量构成的平行四边形的有向面积
AxB ,如果有A在B的逆时针方向(不超180度),那么面积是负的。否则是正的。
https://zhidao.baidu.com/question/562549647.html
设置eps 1e-7~1e-10

int Fabs(double t){ if(fabs(t)<eps) return 0; if(t>0) return 1; return -1; }
叉积算平行四边形面积,然后除以底的长度,得到高(距离)

double hei(po p,po a,po b){ vec t1=vec(a-b),t2=vec(p-b); return fabs(cross(t1,t2))/dis(a,b); }
点积判断和端点形成的角是否是钝角。是钝角,就只能是和线段两个端点的距离取min
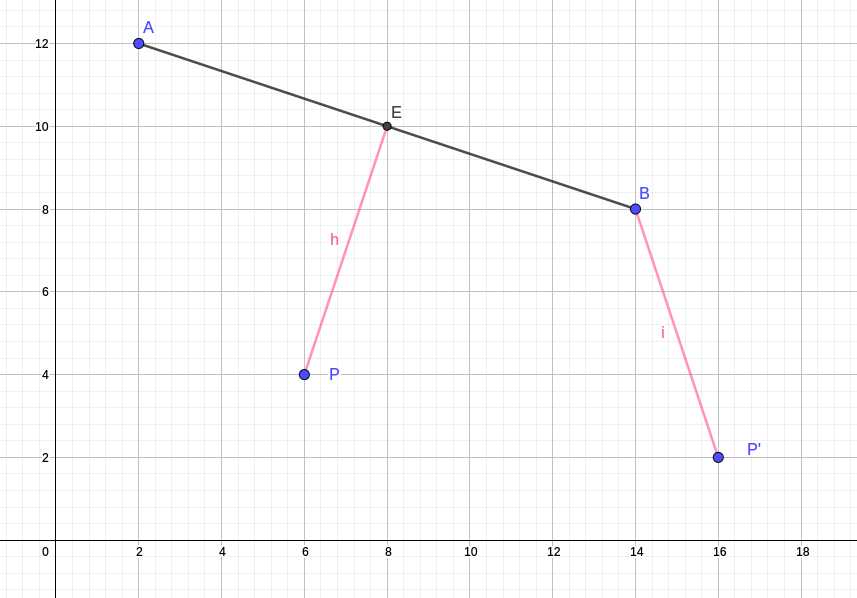
跨立实验
如果两个线段端点互相都在对方的两侧,那么相交。
原文:https://www.cnblogs.com/Miracevin/p/10013826.html