假设函数:
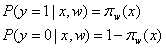
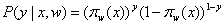 (1)
(1)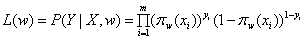
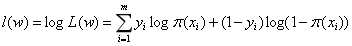
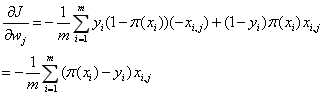
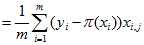 (4)
(4)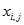 表示第i个样本的第j个属性的取值。
表示第i个样本的第j个属性的取值。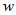 的更新方式为:
的更新方式为: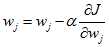 (5)
(5)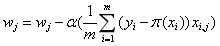 (6)
(6)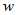
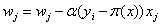 (7)
(7)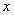
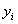 是其真实值,
是其真实值,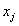 是这个样本的第j个属性
是这个样本的第j个属性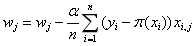 (8)
(8)logistic回归算法的损失函数:binary_crossentropy(二元交叉熵)
原文:https://www.cnblogs.com/sunrise-keephungary/p/10056027.html