噩梦般的算法...反正考场上不指望调对了
怕什么lz还写过300多行的次小生成树呢
模板:洛谷P3384
看到题目,是不是觉得似曾相识?
我们把这道题拆分一下(操作3和4暂时不管)
如果只有操作1,你会想到,这可以用树上差分来维护
如果只有操作2,树上倍增lca大水题
那么把两个结合起来就是我们现在看到的这道题目...
怎么做呢?
我们想,这道题跟线段树版题又挺像的,只是变到了树上
那么是不是可以把这棵树拆成许多条链,每条链用线段树(或其他数据结构)进行维护,最后再把所有经过的链的答案加起来呢?
这就是树链剖分。
算一下,单次修改或查询的时间复杂度为O(k*logn),k是经过的链的条数
又一个问题来了:怎么去拆分这棵树,使得k尽可能小呢?
有很多种方法,这里介绍轻重链拆分法 其他的我不会,它可以保证从树上一点到另一点经过的链的条数不超过logn条,所以单次O((logn)^2)
为啥不超过logn条呢?
emm...我不会,你们自己百度吧(有时间也许会填坑的)
首先明确几个名词:(引用自ivanovcraft)
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
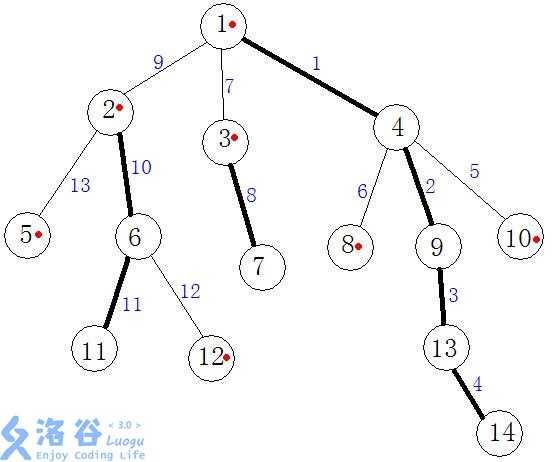
上图中加粗的边就是重边
图中所有的重链就是我们分出来的链,特别的,没有被重链覆盖的单个节点也看做一条链来维护
因为链与链之间互不干扰,所以实际上只需要建一颗线段树就可以维护所有链了!
这涉及到线段树中节点序号的问题。我们需要让重链上的节点的新序号是连续的,这样才能用线段树维护
我们将会使用2遍dfs完成对这棵树的拆分
第一遍dfs,处理出每个节点的父亲(prt)、深度(dep)、大小(size),以及他的重儿子(son)
第二遍dfs,处理每个节点所在重链的顶部节点编号(top),还有在线段树中的新编号(rk)。遍历时优先进入重儿子,保证重链编号的连续。
这样就拆分完了。其实树链剖分的主体并不长。
拆分完了,就该处理修改和查询了。以查询为例
比较两个节点的top的深度,选择深度较大的那一个节点,上跳到它top的父亲那里去。如果top是根节点就不跳了
在这个过程中把上跳的这一段用线段树求和,加到ans里。
循环往复,直到两个节点的top相同,说明他们在同一条重链里了,此时在加入他们之间节点的和,bingo!
修改和查询差不多,就不多说了
回头看操作3和操作4,对子树的统一操作,这不更简单吗?
我们的遍历是保证了子树里的所有节点的新编号是连续的,所以直接对线段树里的rk[id]~rk[id]+size[id]-1操作就行了

#include<iostream> #include<cstdio> #include<cmath> #include<cstring> #include<algorithm> #include<ctime> #include<cstdlib> #include<queue> using namespace std; struct SegTree{//线段树 struct Node{ long long l,r,val,lazy; }tree[400000]; long long size; void build(long long id,long long l,long long r){ tree[id]=(Node){l,r,0,0}; if(l==r) return ; long long mid=(l+r)/2; build(id*2,l,mid); build(id*2+1,mid+1,r); } void lazydown(long long id){ long long lc=id*2,rc=id*2+1,lazy=tree[id].lazy; tree[lc].lazy+=lazy; tree[lc].val+=(tree[lc].r-tree[lc].l+1)*lazy; tree[rc].lazy+=lazy; tree[rc].val+=(tree[rc].r-tree[rc].l+1)*lazy; tree[id].lazy=0; } long long al,ar,aval; void update(long long id){ long long l=tree[id].l,r=tree[id].r; if(al<=l&&r<=ar){ tree[id].lazy+=aval; tree[id].val+=(r-l+1)*aval; return ; } if(tree[id].lazy!=0) lazydown(id); long long mid=(l+r)/2; if(al<=mid) update(id*2); if(ar>mid) update(id*2+1); tree[id].val=tree[id*2].val+tree[id*2+1].val; } void afo(long long id){//别问我这个函数名是什么鬼 long long l=tree[id].l,r=tree[id].r; if(al<=l&&r<=ar){ aval+=tree[id].val; return ; } if(tree[id].lazy!=0) lazydown(id); long long mid=(l+r)/2; if(al<=mid) afo(id*2); if(ar>mid) afo(id*2+1); } //for user void init(long long mys){ size=mys; build(1,1,size); } void change(long long l,long long r,long long val){ al=l;ar=r;aval=val; update(1); } long long ask(long long l,long long r){ al=l;ar=r;aval=0; afo(1); return aval; } }; long long n,qn,root,MOD; struct star{//链式前向星存树 long long u,v; }edge[400000]; long long last[400000],nxt[400000],m; void addedge(long long u,long long v){ m++; edge[m]=(star){u,v}; nxt[m]=last[u]; last[u]=m; } long long prt[400000],dep[400000],size[400000], son[400000],top[400000],rk[400000],rkn; void dfs1(long long id,long long fa,long long d){//第一遍dfs,处理prt,dep,size,son prt[id]=fa; dep[id]=d; size[id]=1; long long fat=-1; for(long long i=last[id];i!=-1;i=nxt[i]){ long long to=edge[i].v; if(to==fa) continue; dfs1(to,id,d+1); size[id]+=size[to]; if(fat==-1) fat=to; else if(size[to]>size[fat]) fat=to; } son[id]=fat; } void dfs2(long long id,long long tp){//第二遍dfs,处理top,rk rkn++;rk[id]=rkn; top[id]=tp; if(son[id]==-1) return; dfs2(son[id],tp); for(long long i=last[id];i!=-1;i=nxt[i]){ long long to=edge[i].v; if(to==prt[id]||to==son[id]) continue; dfs2(to,to); } } SegTree seg; void change(long long px,long long py,long long val){//操作1 for(;top[px]!=top[py];){ if(dep[top[px]]<dep[top[py]]) swap(px,py);//注意应比较top[px]和top[py]的深度,而不是px和py的深度 long long fx=top[px],fy=top[py]; if(prt[fx]!=-1){//如果top不是根节点 seg.change(rk[fx],rk[px],val); px=prt[fx]; } } if(rk[px]>rk[py]) swap(px,py);//就是这里忘swap了害得我调了1hour seg.change(rk[px],rk[py],val); } long long ask(long long px,long long py){//操作2 long long ans=0; for(;top[px]!=top[py];){ if(dep[top[px]]<dep[top[py]]) swap(px,py); long long fx=top[px],fy=top[py]; if(prt[fx]!=-1){ ans+=seg.ask(rk[fx],rk[px]); px=prt[fx]; } } if(rk[px]>rk[py]) swap(px,py); ans+=seg.ask(rk[px],rk[py]); return ans; } long long stv[400000]; int main(){ cin>>n>>qn>>root>>MOD; seg.init(n); for(long long i=1;i<=n;i++){ scanf("%lld",&stv[i]); } m=0; for(long long i=1;i<=n;i++) last[i]=-1; for(long long i=1;i<=n-1;i++){ long long u,v; scanf("%lld%lld",&u,&v); addedge(u,v); addedge(v,u); } dfs1(root,-1,1); rkn=0; dfs2(root,root); for(long long i=1;i<=n;i++){ seg.change(rk[i],rk[i],stv[i]); } for(long long i=1;i<=qn;i++){ long long type,l,r,val; scanf("%lld",&type); switch(type){ case 1:{ scanf("%lld%lld%lld",&l,&r,&val); change(l,r,val); break; } case 2:{ scanf("%lld%lld",&l,&r); printf("%lld\n",ask(l,r)%MOD); break; } case 3:{ scanf("%lld%lld",&l,&val); r=rk[l]+size[l]-1; l=rk[l]; seg.change(l,r,val); break; } case 4:{ scanf("%lld",&l); r=rk[l]+size[l]-1; l=rk[l]; printf("%lld\n",seg.ask(l,r)%MOD); break; } } } return 0; }
<summary>lca也可以用树剖</summary>
参考:https://www.cnblogs.com/ivanovcraft/p/9019090.html
原文:https://www.cnblogs.com/sun123zxy/p/treedividing.html