网络流24题 gay题报告

时间：2018-12-04 16:34:47 阅读：168 评论：0 收藏：0 [点我收藏+]

洛谷上面有一整套题。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

①飞行员配对方案问题。

裸二分图匹配。

 1 #include <cstdio>
 2 
 3 const int N = 110, M = 10010;
 4 
 5 struct Edge {
 6     int nex, v;
 7 }edge[M << 1]; int top;
 8 
 9 int n, m, e[N], mat[N], vis[N], Time;
10 
11 inline void add(int x, int y) {
12     top++;
13     edge[top].v = y;
14     edge[top].nex = e[x];
15     e[x] = top;
16     return;
17 }
18 
19 bool DFS(int x) {
20     for(int i = e[x]; i; i = edge[i].nex) {
21         int y = edge[i].v;
22         if(vis[y] == Time) {
23             continue;
24         }
25         vis[y] = Time;
26         if(!mat[y] || DFS(mat[y])) {
27             mat[y] = x;
28             return 1;
29         }
30     }
31     return 0;
32 }
33 
34 int main() {
35     scanf("%d%d", &m, &n);
36     int x, y;
37     while(scanf("%d%d", &x, &y)) {
38         if(x == -1 && y == -1) {
39             break;
40         }
41         add(x, y);
42         add(y, x);
43     }
44 
45     int ans = 0;
46     for(int i = 1; i <= m; i++) {
47         Time = i;
48         if(DFS(i)) {
49             ans++;
50         }
51     }
52 
53     if(!ans) {
54         printf("No Solution!");
55         return 0;
56     }
57 
58     printf("%d\n", ans);
59     for(int i = m + 1; i <= n; i++) {
60         if(mat[i]) {
61             printf("%d %d", mat[i], i);
62             ans--;
63             if(ans) {
64                 puts("");
65             }
66         }
67     }
68 
69     return 0;
70 }

匈牙利AC代码

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 10010, M = 100010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N];
 13 std::queue<int> Q;
 14 
 15 inline void add(int x, int y, int z) {
 16     top++;
 17     edge[top].nex = e[x];
 18     edge[top].v = y;
 19     edge[top].c = z;
 20     e[x] = top;
 21     return;
 22 }
 23 
 24 inline bool BFS(int s, int t) {
 25     memset(d, 0x3f, sizeof(d));
 26     d[s] = 1;
 27     Q.push(s);
 28     while(!Q.empty()) {
 29         int x = Q.front();
 30         Q.pop();
 31         for(int i = e[x]; i; i = edge[i].nex) {
 32             int y = edge[i].v;
 33             if(edge[i].c && d[y] == INF) {
 34                 d[y] = d[x] + 1;
 35                 Q.push(y);
 36             }
 37         }
 38     }
 39     return d[t] < INF;
 40 }
 41 
 42 int DFS(int x, int t, int maxF) {
 43     if(x == t) {
 44         return maxF;
 45     }
 46     int ans = 0;
 47     for(int i = e[x]; i; i = edge[i].nex) {
 48         int y = edge[i].v;
 49         if(d[x] + 1 != d[y] || !edge[i].c) {
 50             continue;
 51         }
 52         int temp = DFS(y, t, std::min(edge[i].c, maxF - ans));
 53         if(!temp) {
 54             d[y] = 0;
 55         }
 56         ans += temp;
 57         edge[i].c -= temp;
 58         edge[i ^ 1].c += temp;
 59         if(ans == maxF) {
 60             return ans;
 61         }
 62     }
 63     return ans;
 64 }
 65 
 66 int solve(int s, int t) {
 67     int ans = 0;
 68     while(BFS(s, t)) {
 69         ans += DFS(s, t, INF);
 70     }
 71     return ans;
 72 }
 73 
 74 int main() {
 75     int n, m;
 76     scanf("%d%d", &m, &n);
 77     int x, y;
 78     while(scanf("%d%d", &x, &y)) {
 79         if(x == -1) {
 80             break;
 81         }
 82         add(x, y, 1);
 83         add(y, x, 0);
 84         //printf("%d %d \n", x, y);
 85     }
 86     int s = n + 1, t = n + 2;
 87     for(int i = 1; i <= m; i++) {
 88         add(s, i, 1);
 89         add(i, s, 0);
 90         //printf("s %d \n", i);
 91     }
 92     for(int i = m + 1; i <= n; i++) {
 93         add(i, t, 1);
 94         add(t, i, 0);
 95         //printf("%d t \n", i);
 96     }
 97 
 98     int ans = solve(s, t);
 99     if(!ans) {
100         printf("No Solution!");
101         return 0;
102     }
103     printf("%d\n", ans);
104     for(int i = 2; i <= top; i += 2) {
105         if(edge[i].c || edge[i ^ 1].v == s || edge[i].v == t) {
106             continue;
107         }
108         printf("%d %d", edge[i ^ 1].v, edge[i].v);
109         ans--;
110         if(ans) {
111             puts("");
112         }
113     }
114 
115     return 0;
116 }

DinicAC代码

②负载平衡问题。

环形均分纸牌。也可以用费用流做。

首先每个人的牌数是sum/n，这点可以建立源汇，用流量来控制。

所以代价交换次数最小就用费用来控制。

相邻之间连边，费用为1，流量INF。

每个点与源连边，流量为一开始的牌数，费用为0。

每个点与汇连边，流量为sum/n，费用为0。

然后跑最小费用最大流。

(这里注意，无向边费用流，对于一条边要建4条边才行。

最大流可以只建两条边，流量都为c，但是费用流的费用要取负，不好搞。)

  1 #include <cstdio>
  2 #include <queue>
  3 #include <cstring>
  4 #include <algorithm>
  5 
  6 const int N = 210, M = 50010, INF = 0x3f3f3f3f;
  7 
  8 struct Edge {
  9     int nex, v, c, len;
 10 }edge[M << 1]; int top = 1;
 11 
 12 int e[N], d[N], pre[N], Time, flow[N];
 13 std::queue<int> Q;
 14 bool vis[M];
 15 
 16 inline void add(int x, int y, int z, int w) {
 17     top++;
 18     edge[top].nex = e[x];
 19     edge[top].v = y;
 20     edge[top].c = z;
 21     edge[top].len = w;
 22     e[x] = top;
 23     top++;
 24     edge[top].v = x;
 25     edge[top].c = 0;
 26     edge[top].len = -w;
 27     edge[top].nex = e[y];
 28     e[y] = top;
 29     return;
 30 }
 31 
 32 inline bool SPFA(int s, int t) {
 33     memset(d, 0x3f, sizeof(d));
 34     d[s] = 0;
 35     vis[s] = Time;
 36     flow[s] = INF;
 37     Q.push(s);
 38     while(!Q.empty()) {
 39         int x = Q.front();
 40         Q.pop();
 41         vis[x] = 0;
 42         for(int i = e[x]; i; i = edge[i].nex) {
 43             int y = edge[i].v;
 44             if(!edge[i].c) {
 45                 continue;
 46             }
 47             if(d[y] > d[x] + edge[i].len) {
 48                 d[y] = d[x] + edge[i].len;
 49                 pre[y] = i;
 50                 flow[y] = std::min(flow[x], edge[i].c);
 51                 //printf("y = %d d = %d flow = %d \n", y, d[y], flow[y]);
 52                 if(vis[y] != Time) {
 53                     vis[y] = Time;
 54                     Q.push(y);
 55                 }
 56             }
 57         }
 58     }
 59     /*for(int i = 1; i <= 7; i++) {
 60         printf("%d %d \n", d[i], flow[i]);
 61     }*/
 62     return d[t] < INF; // error 0
 63 }
 64 
 65 inline void update(int s, int t) {
 66     int f = flow[t], i = pre[t];
 67     while(t != s) {
 68         edge[i].c -= f;
 69         edge[i ^ 1].c += f;
 70         t = edge[i ^ 1].v;
 71         i = pre[t];
 72     }
 73     return;
 74 }
 75 
 76 int solve(int s, int t, int &cost) {
 77     int ans = 0;
 78     cost = 0;
 79     Time = 1;
 80     while(SPFA(s, t)) {
 81         ans += flow[t];
 82         cost += flow[t] * d[t];
 83         update(s, t);
 84         Time++;
 85         //printf("%d %d \n", ans, cost);
 86     }
 87     return ans;
 88 }
 89 
 90 int main() {
 91     int n, sum = 0;
 92     scanf("%d", &n);
 93     int s = n + 1, t = n + 2;
 94     for(int i = 1, x; i <= n; i++) {
 95         scanf("%d", &x);
 96         sum += x;
 97         if(i > 1) {
 98             add(i, i - 1, INF, 1);
 99         }
100         if(i < n) {
101             add(i, i + 1, INF, 1);
102         }
103         add(s, i, x, 0);
104     }
105     add(1, n, INF, 1);
106     add(n, 1, INF, 1);
107     sum /= n;
108     for(int i = 1; i <= n; i++) {
109         add(i, t, sum, 0);
110     }
111 
112     int ans, cost;
113     ans = solve(s, t, cost);
114     printf("%d", cost);
115     return 0;
116 }

AC代码

③软件补丁问题。

?(?>?<?)?

这题看了一会，想到一个状压+SPFA转移的做法，算一下复杂度好像不行，但是没有别的算法了....

跑去看题解，还真是？？！！

弃疗了。

④魔术球问题。

这题，我有个非常SB的二分费用流！

然后果断T掉......

没事，我会动态加点！然后加出负环来了...GG。

负环如下：

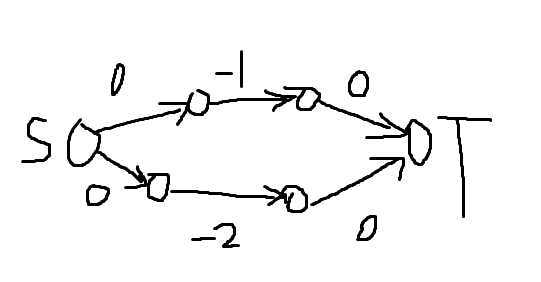
技术分享图片

图中所有流量为1，数字表示费用。先加上面三条边，然后跑一遍，然后加下面三条边再跑。

可以发现此时出现了流量为1的负环.......

然后跑去看题解，嗯？？？最小路径覆盖？(我傻了。)

然后按照题解的方法

网络流24题 gay题报告

原文：https://www.cnblogs.com/huyufeifei/p/10064509.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)