l ROC曲线
|
预测 |
|
|
|
||||
|
|
|
|
1 |
0 |
合计 |
||
|
实际 |
1 |
|
|
|
True Positive(TP) |
False Negative(FN) |
Actual Positive(TP+FN) |
|
0 |
|
|
|
False Positive(FP) |
True Negative(TN) |
Actual Negative(FP+TN) |
|
|
合计 |
|
|
|
Predicted Positive(TP+FP) |
Predicted Negative(FN+TN) |
TP+FP+FN+TN |
于是我们得到四个指标,分别为:真阳、伪阳、伪阴、真阴。
ROC空间将伪阳性率(FPR)定义为 X 轴,真阳性率(TPR)定义为 Y 轴。
这两个值由上面四个值计算得到,公式如下:
TPR:在所有实际为阳性的样本中,被正确地判断为阳性之比率。TPR=TP/(TP+FN)
FPR:在所有实际为阴性的样本中,被错误地判断为阳性之比率。FPR=FP/(FP+TN)
放在具体领域来理解上述两个指标。如在医学诊断中,判断有病的样本。那么尽量把有病的揪出来是主要任务,也就是第一个指标TPR,要越高越好。而把没病的样本误诊为有病的,也就是第二个指标FPR,要越低越好。不难发现,这两个指标之间是相互制约的。如果某个医生对于有病的症状比较敏感,稍微的小症状都判断为有病,那么他的第一个指标应该会很高,但是第二个指标也就相应地变高。最极端的情况下,他把所有的样本都看做有病,那么第一个指标达到1,第二个指标也为1。
l AUC
AUC值为ROC曲线所覆盖的区域面积,显然,AUC越大,分类器分类效果越好。
AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
0.5 < AUC < 1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
l P-R & F1
precision查准率:判定为正例的样本当中有多少实际为真
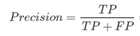
Recall查全率或召回率:被正确分类的样本中有多少为真
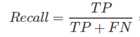
F1调和平均:
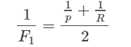
Fβ加权调和平均:
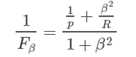
β>1: Recall(查全)有更大影响, 宁可错杀无辜也不能放过坏人
β<1: Precision(查准)有更大影响, 尽可能一查一个准减少冤假错案
原文:https://www.cnblogs.com/yongfuxue/p/10095434.html