RNN的发源:
单层的神经网络(只有一个细胞,f(wx+b),只有输入,没有输出和hidden state)
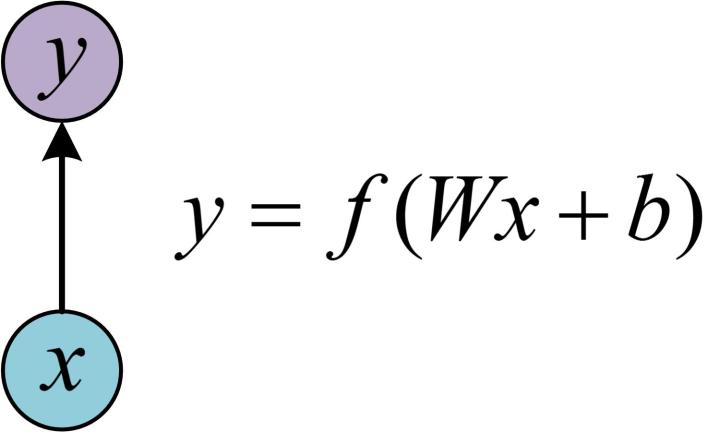
多个神经细胞(增加细胞个数和hidden state,hidden是f(wx+b),但是依然没有输出)
这里RNN同时和当前的输入有关系,并且是上一层的输出有关系。
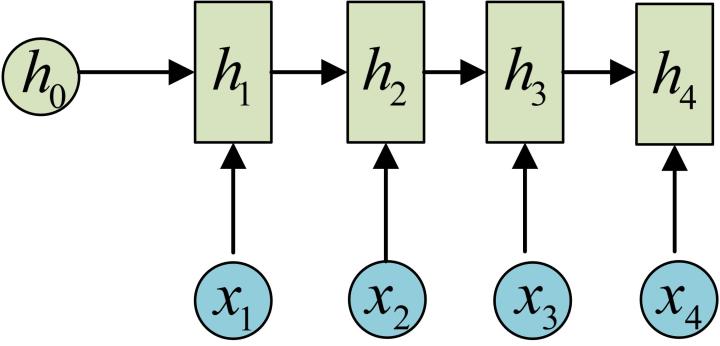
初步的RNN(增加输出softmax(Wx+b),输出和hidden state的区别是对wx+b操作的函数不同)
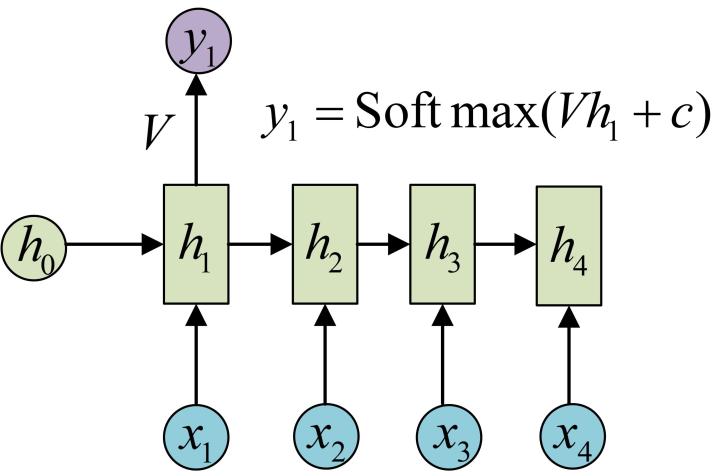
备注多层的神经细胞和全连接层的区别:
全连接层只有:输入、输出和权重矩阵, 如下图。
初步的RNN和普通意义上的全连接层的区别是:RNN的输出和输入、上一层的hidden state有关。这也是RNN最大的优点,能够利用上一时刻的输出来修正下一时刻的输入。
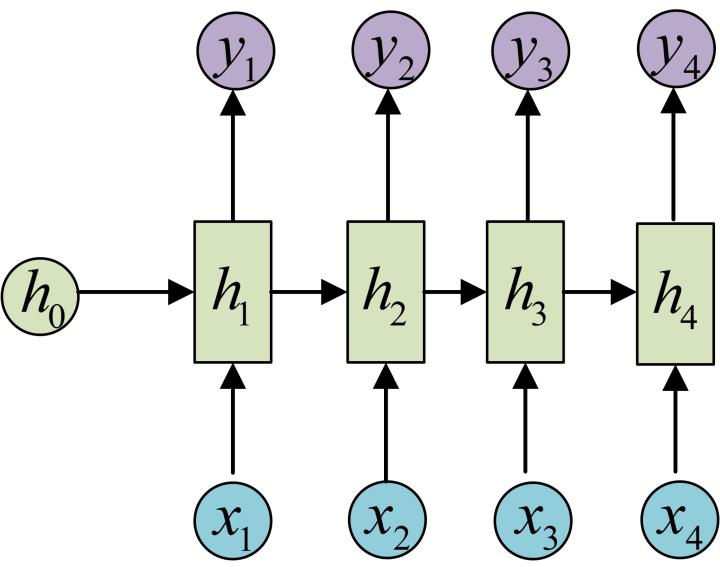
这是现在普遍流行的RNN神经网络
优点:将当前的输出和上一时刻的输出结合起来。充分模拟了人思考的过程,比如例如当你读一篇文章的时候,你会根据对之前单词的理解来理解后面的每一个单词。你不会抛掉之前所知的一切而重新开始思考。思维是有持久性的。
缺点:
更长时间的信息会随着神经网络的层数增多而慢慢消失。
使用tanh作为激活函数存在梯度消失的问题。
应用:在不仅仅要临近信息的场景,比如预测北京明天的空气质量,明天的空气质量受今天天气的影响最大,不需要更长时间内的信息,所以用RNN效果更好,但是要更长时间内的影响,则用LSTM模型效果更好。
备注:经常的使用f(wx+b)的激活函数是tanh。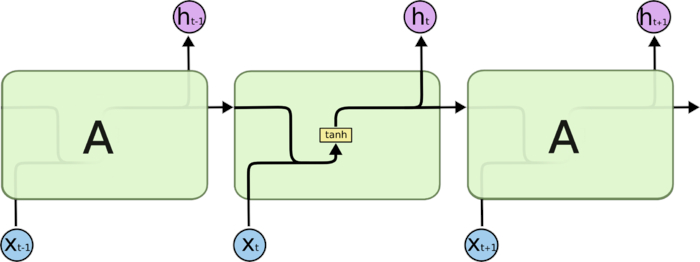
针对RNN不能记忆长时间内容的问题,提出了LSTM(长短期记忆网络),具有对长期记忆学习的能力。
LSTM完整的神经网络构造图
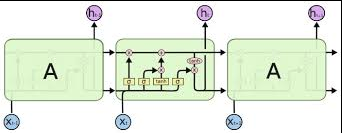
主要包含:
对比RNN:
输入上增加了cell state,cell内部增加了三个门,分别控制cell state和hidden state。

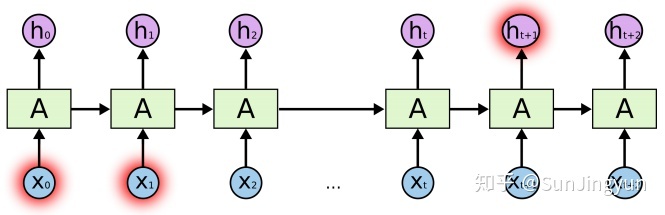
上图是RNN的神经网络图

上图是
将信息流的状态分成cell state和input state。主线是cell state,直接在整个细胞上运行,只有一些少量的线性交互,主要维持信息不变。分线是gate控制的input state,向cell state添加或者删除信息。
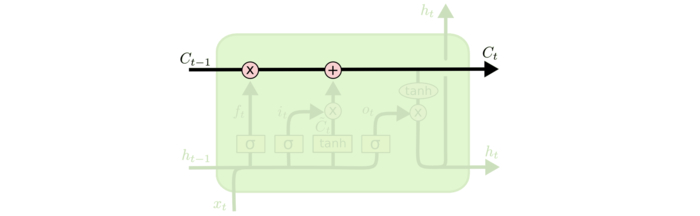
上图是整个LSTM的信息流动图
本质是之前的语句对全局的重要性。
原理:通过当前时刻的输入和上一时刻的hidden state决定要保留多少信息。
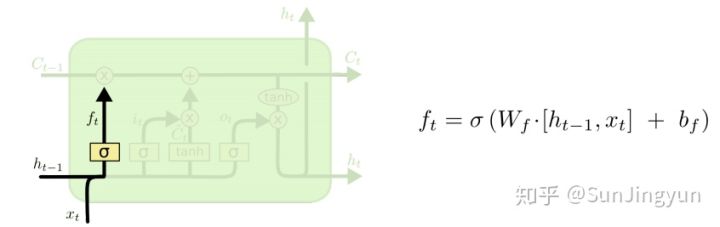
上图是遗忘门的示意图
遗忘门计算公式:\(f_t=σ(W_f \cdot [h_{t-1},x_t]+b_f)\)
\(W_f\) 是遗忘门的权重矩阵,
\(b_f\) 是遗忘门的偏置项,
σ 是 sigmoid 函数。
\([h_{t-1}, x_t]\) 表示把两个向量连接成一个更长的向量,
原先的函数形式是 \(σ(w \cdot x+b)\),转变为现在的 \(σ(w \cdot x+w \cdot h)+b = σ (w([h,x])+b)\)
这里的所有输出都是hidden state拼接x形成的向量
本质是判断当前词语对全局的重要性。
原理:通过短期记忆和长期记忆控制当前的输入进入cell state。感觉就像是控制了输入的进入比例,和当前的cell state状态
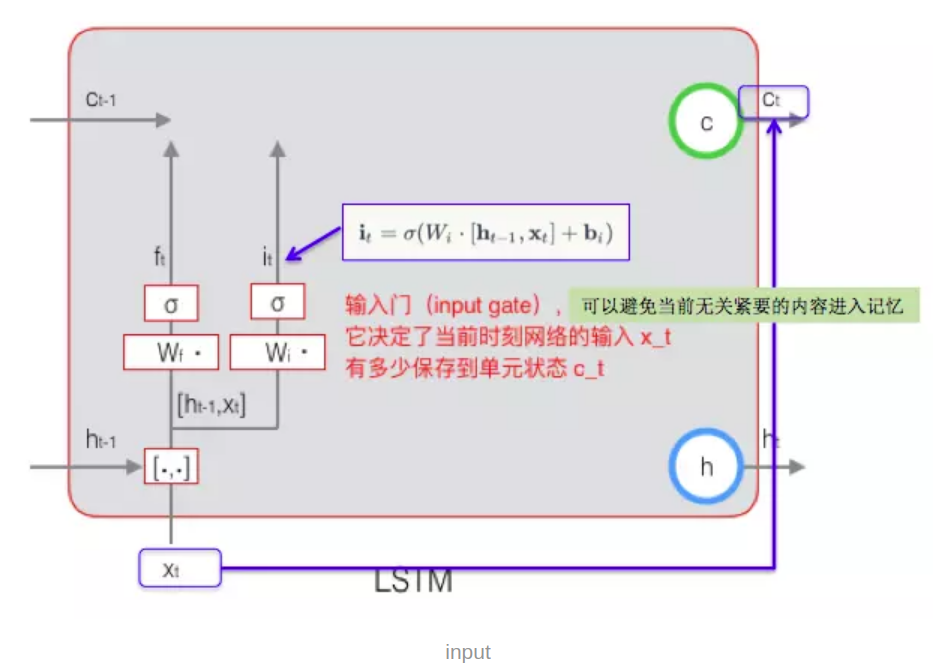
输入门的示意图
本质是判断当前的内容对后续语句的重要性。
原理: 输出门主要输出cell state和hidden state。
cell state结果=保留比例\(c_{i-1}\)+输入比例输入内容
hidden state结果=输出比例*tanh(cell state)
保留比例:遗忘门控制(sigmoid函数)
输出比例:输入门控制(sigmoid函数)
输出比例:输出门控制(sigmoid函数)
输出分为两个部分:cell state和hidden state
\(c_t = f_t \cdot c_{t-1} + i_t \cdot \tilde{c_t}\)
其中:\(f_t = σ(W_f \cdot [h_{t-1},x_t]+b_f)\) (遗忘门的计算方式)
\(c_{t-1}\) 是上一时刻的细胞状态
$i_t \(是输入门,\)i_t = σ(W_i \cdot [h_{t-1},x_t]+b_i)$
\(\tilde{c_t}\)当前输入的细胞状态,\(\tilde{c_t} = tanh(W_c \cdot [h_{t-1},x_t]+b_c)\)
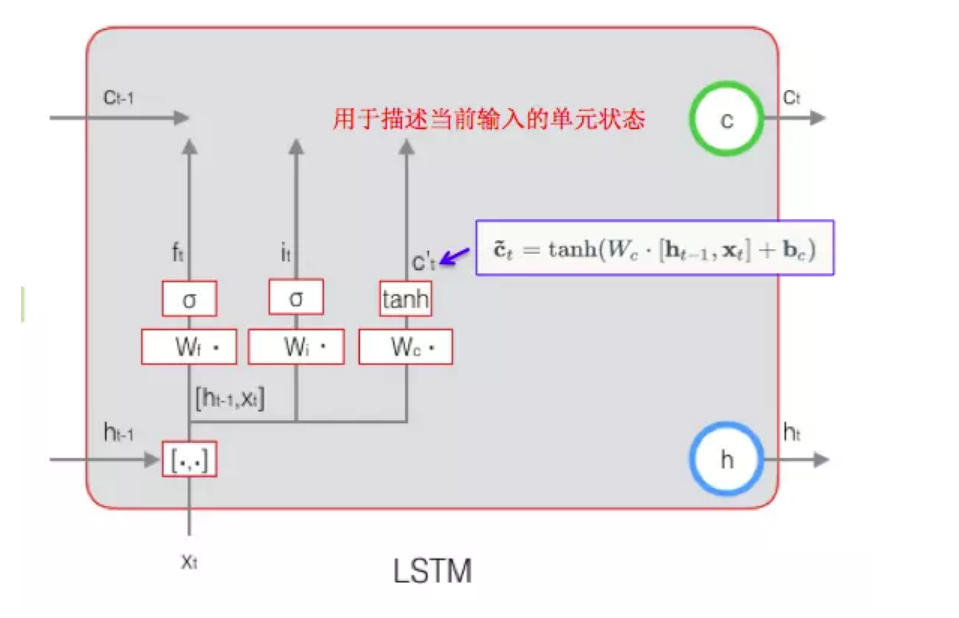
当前\(\tilde{c_t}\) 计算示意图
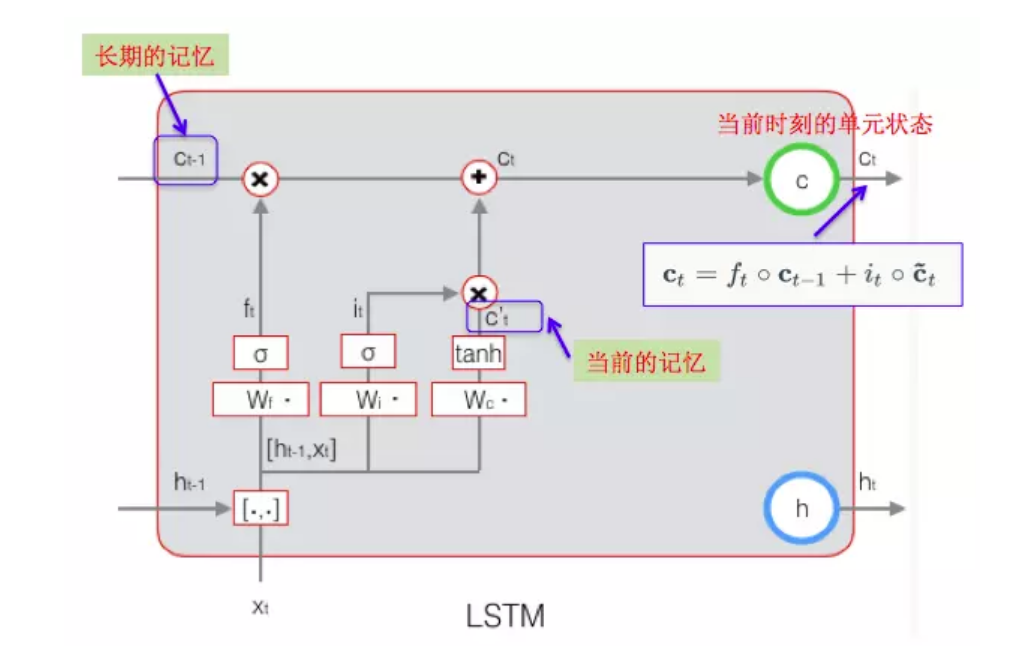
当前\(c_t\)计算示意图
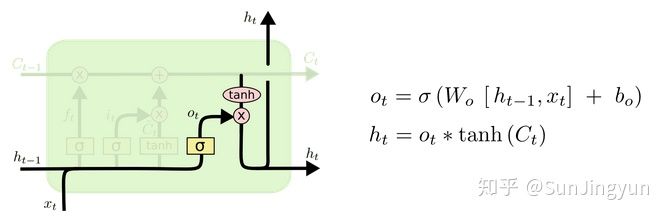
上图是输出示意图
解决了RNN梯度消失的问题
自我认为:LSTM存在梯度消失的问题,因为最后hidden state输出: \(h_i=o_t*tanh(f_t*c_{i-1}+i_i*\sigma(w_i[h,x]+b_i))\),引起梯度消失的两条途径是:激活函数和连式法则,这里使用了tanh函数,所以存在梯度消失的可能性。
但是网上大多数认为不存在梯度消失。因为在RNN的梯度传导过程中,如果某次w出现极小值,再乘以sigmoid函数,w的数值会越来越小。但是在LSTM的传导中,如果某次出现了极小值,但是下一次的cell state不一定会是极小的,因为cell state来源与两部分:上一次的cell state和input,即使是cell state出现极小值,但是input仍然不会存在极小值,所以下一次的cell state的不一定会出现极小值,所以w不会继续变小。
具有记忆功能
这个是在RNN就解决的问题,就是因为有递归效应,上一时刻隐层的状态参与到了这个时刻的计算过程中,直白一点呢的表述也就是选择和决策参考了上一次的状态。
LSTM记的时间长
因为gate的特点,误差向上一个上一个状态传递时几乎没有衰减,所以权值调整的时候,对于很长时间之前的状态带来的影响和结尾状态带来的影响可以同时发挥作用,最后训练出来的模型就具有较长时间范围内的记忆功能。
LSTM非常适合用于处理与时间序列高度相关的问题,例如机器翻译、对话生成、编码、解码等
在经典的循环神经网络中,状态的传输是从前往后单向的。然而,在有些问题中,当前时刻的输出不仅和之前的状态有关系,也和之后的状态相关。我_ _ 想吃羊肉,要预测空格中的词语要同时看前后的词语的意思和时态、词性。这时就需要双向RNN(BiRNN)来解决这类问题。
双向RNN是由两个RNN上下叠加在一起组成的。输出由这两个RNN的状态共同决定。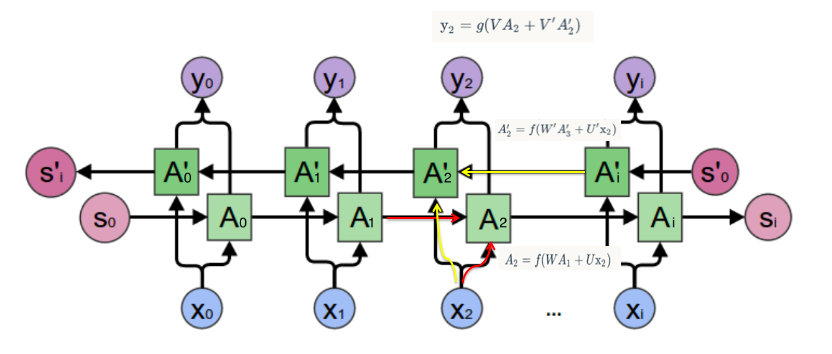
其中,正向计算时,隐藏层的 \(s_t\) 与 \(s_{t-1}\) 有关;反向计算时,隐藏层的 \(s_t\) 与 \(s_{t+1}\) 有关。
在预测中,当前字词的预测不仅取决于前面已经翻译的字词,还取决于原始的输入。这决定了cell需要将之前cell的state和output。同时,我们知道在以往的语句生成中,cell的output被当做生成的语句,那么生成的语句就会和input语句的长度一致。但是这是违反常规的,所以提出了Seq2Seq模型,分成encoder和decoder模型,可以使输入语句和输出语句的长度不一样。Seq2Seq最早被应用于机器翻译,后来扩展到多种NLP任务。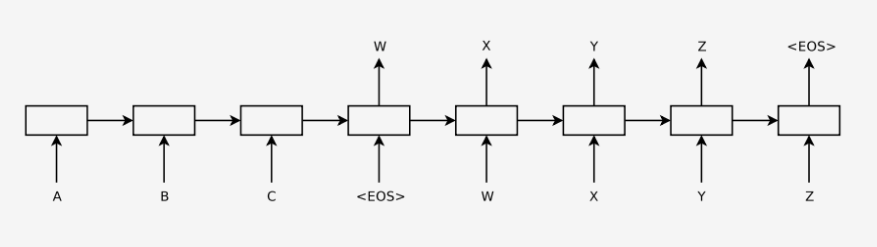
这是Seq2Seq的总体流程图,把encoder最后一个时刻的cell 的hidden state 输出到decoder的第一个cell里,通过激活函数和softmax层,得到候选的symbols,筛选出概率最大的symbols,作为下一个cell的输入。汇总所有的decoder的output就是最后的预测结果。
为什么要使用Encoder的最后一个hidden state?
在Encoder-Decoder结构中,Encoder把所有的输入序列都编码成一个统一的语义特征c再解码,因此, c中包含原始序列中的所有信息。
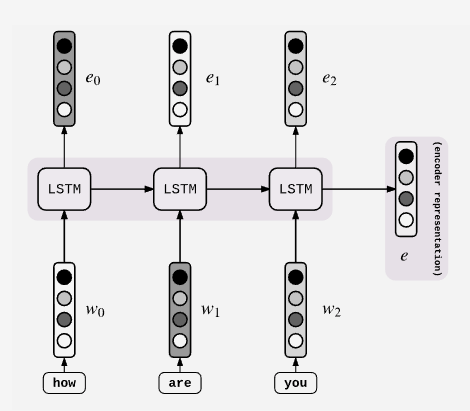
这是Encoder的构造,它和普通的RNN、LSTM没有区别。具体每个细胞接受的是每一个单词word embedding,和上一个时间点的hidden state。输出的是这个时间点的hidden state。
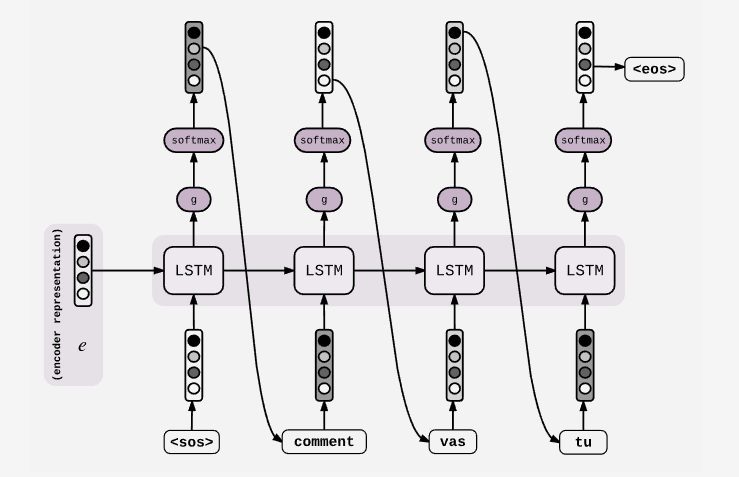
这是Decoder的构造,第一个cell是输入是encode的最后一个cell的hidden state,并且当前的output会输入到下一个cell中。
由于encoder-decoder模型在编码和解码阶段始终由一个不变的语义向量C来联系着,编码器要将整个序列的信息压缩进一个固定长度的向量中去。这就造成了 (1)语义向量无法完全表示整个序列的信息,(2)最开始输入的序列容易被后输入的序列给覆盖掉,会丢失许多细节信息。在长序列上表现的尤为明显。 引入Attention
: 相比于之前的encoder-decoder模型,attention模型最大的区别就在于它不在要求编码器将所有输入信息都编码进一个固定长度的向量之中。相反,此时编码器需要将输入编码成一个向量的序列,而在解码的时候,每一步都会选择性的从向量序列中挑选一个子集进行进一步处理。这样,在产生每一个输出的时候,都能够做到充分利用输入序列携带的信息。而且这种方法在翻译任务中取得了非常不错的成果。
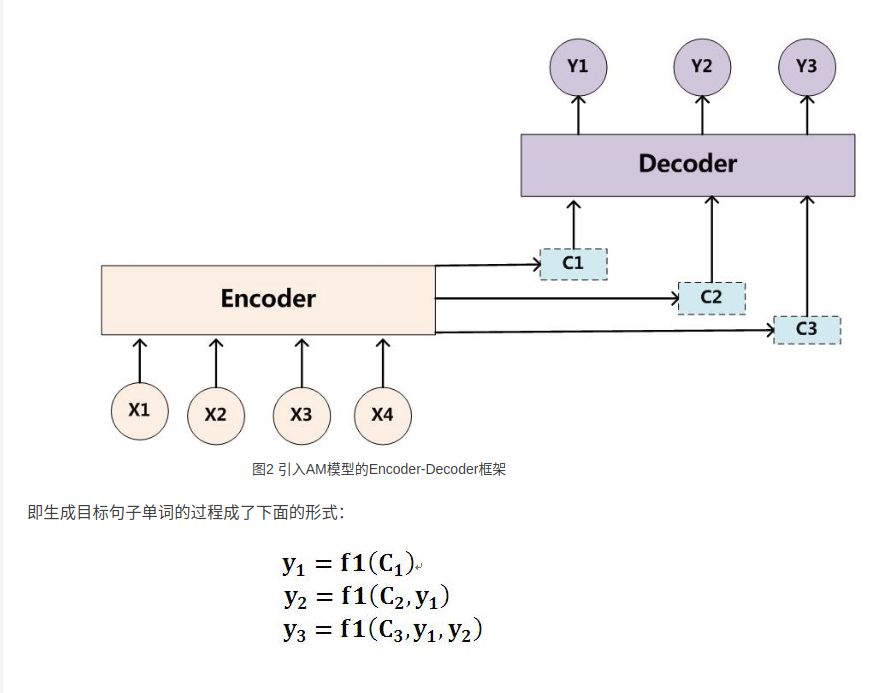
上图是Seq2Seq模型+Attentionmo模型的完整示意图。
现在的解码过程(Decoder)是:
预测当前词\(y_i\)需要当前时刻的\(h_i\)和\(c_i\)上下文向量和上一时刻的输出\(y_i\)
预测当前词的\(h_i\)需要上一时刻的\(h_{i-1},y_{i-1}\)和\(C_i\)

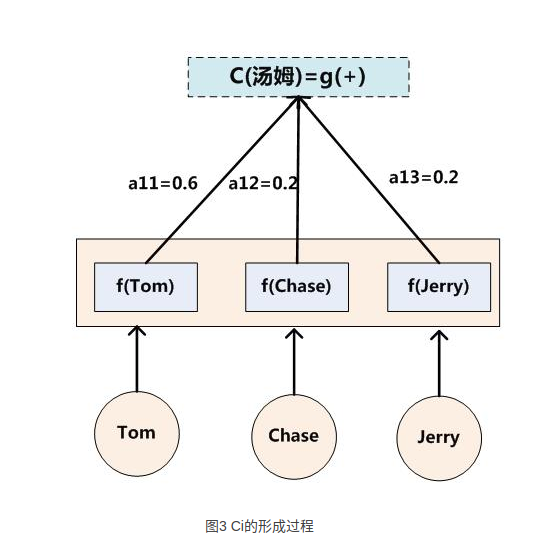
上图是计算\(c_i\)的完整过程示意图
其中:\(c_i=\sum_{j=1}^{T_x}{\alpha_{ij}h_j}\),
\(T_x\)表示Encoder输入文本的长度,
\(i\) 表示预测的第i个字符,
\(j\) 表示Encoder中第j个字符,
\(\alpha_{ij}\) 表示:输入Encoder中的第j个字符对预测第i个字符的影响程度,
\(h_j\) 表示输入Encoder的第j个字符的hidden state。
这个计算公式的本质意义就是将输入字符的hidden state加权。重点是权重的计算方式。
上图是计算\(c_i\)的图形过程示意图,之前的计算过程表示成图形就是这个样子的。
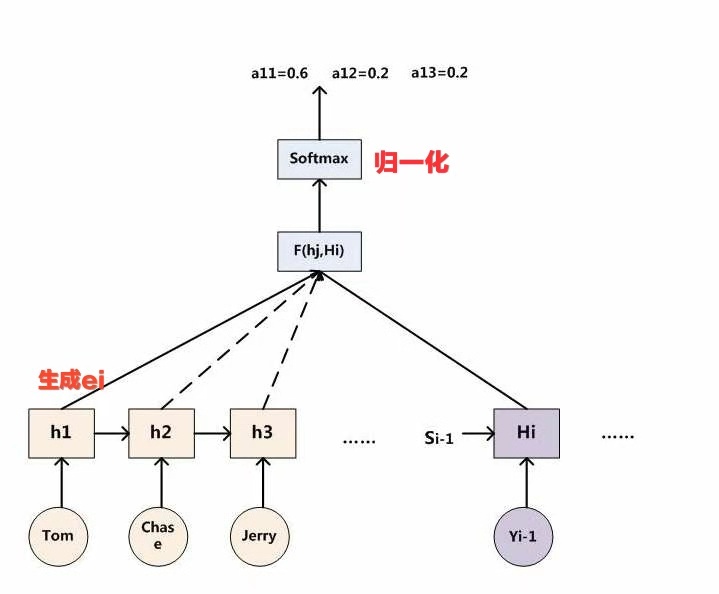
\(\alpha_{ij}=\frac{exp(e_{ij})}{\sum_{k=1}^{T_x}{exp(e_{ik})}} \quad\),底下分母的意义就是归一化
\(e_{ij}=a(y_{i-1,h_j})\),意义就是将已经得到的预测输出和输入Encoder的文字做匹配计算,得到i时刻的输出和j时刻的输入之间的注意力分配关系。最后带入上一个公式计算\(c_i\).
就是我们刚才举例的模型,使用输入Encoder的所有hidden state加权取平均。使用概率抽样的方式,选择某个hiddenstate,估计梯度的时候也采用蒙特卡洛抽样的方法。一般RNN运行的两种mode:(1). Free-running mode;(2). Teacher-Forcing mode[22]。前者就是正常的RNN运行方式:上一个state的输出就做为下一个state的输入,这样做时有风险的,因为在RNN训练的早期,靠前的state中如果出现了极差的结果,那么后面的全部state都会受牵连,以至于最终结果非常不好也很难溯源到发生错误的源头,而后者Teacher-Forcing mode的做法就是,每次不使用上一个state的输出作为下一个state的输入,而是直接使用ground truth的对应上一项作为下一个state的输入。
就拿Seq2Seq模型来举例,我们假设正输出到第三项,准备生成第四项:
nput = ['a', 'b', 'c', 'e', 'f', 'g', 'h']
output = ['o', 'p', 's', ...]
label = ['o', 'p', 'q', 'r', 's', 't', 'u']Free-running mode下的decoder会将第三项错误的输出 output[2] = ‘s‘(下标从0开始)作为下一个state的输入,而在Teacher-forcing mode下,decoder则会将正确样本的第三项 label[2] = ‘q‘ 作为下一个state的输入。 当然这么做也有它的缺点,因为依赖标签数据,在training的时候会有较好的效果,但是在testing的时候就不能得到ground truth的支持了。最好的结果是将Free-running mode的behavior训练得尽可能接近于Teacher-forcing mode。
在测试阶段,decoder的过程有两种主要的解码方式。第一种方法是贪婪解码,它将在上一个时间步预测的单词feed给下一步的输入,来预测本个时间步长的最有可能的单词。
但是,如果有一个cell解码错了词,那么错误便会一直累加。第二种是可能解码方式,也就是beam-search的方法。即在decoder阶段,某个cell解码时不只是选出预测概率最大的symbol,而是选出k个概率最大的词(例如k = 5,我们称k=5为beam-size)。在下一个时间步长,对于这5个概率最大的词,可能就会有5V个symbols(V代表词表的大小)。但是,只保留这5V个symbols中最好的5个,然后不断的沿时间步长走下去。这样可以保证得到的decode的整体的结果最优。
是一种利用句子之间顺序的半监督模型,利用一个encoder和两个decoder,同时预测句子的上一句和下一句,训练目标是使预测的上一句和下一句和label数据的error最小。
难点:句子的上一句和下一句可能的搭配情况非常多,即使是对于人来说也猜测上一句和下一句也是非常困难的事情,更何况是机器。
RNN、LSTM、Seq2Seq、Attention、Teacher forcing、Skip thought模型总结
原文:https://www.cnblogs.com/x739400043/p/10098614.html