正则化

L1范数

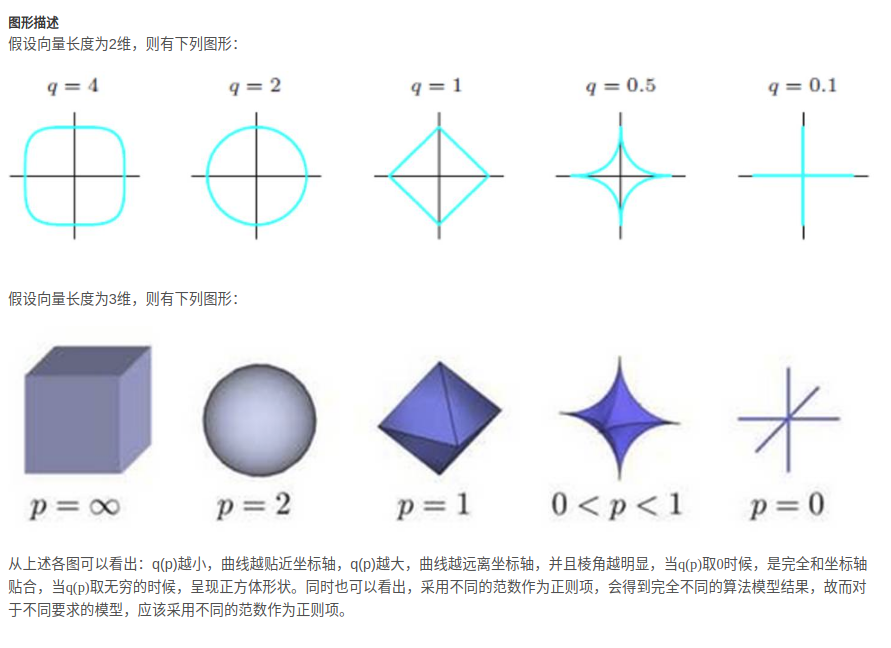
蓝色的是范数的解空间,红色的是损失函数的解空间.L2范数和损失函数的交点处一般在坐标轴上,会使\(\beta=0\),当然并不一定保证交于坐标轴,但是通过实验发现大部分可以得到稀疏解.

L2范数

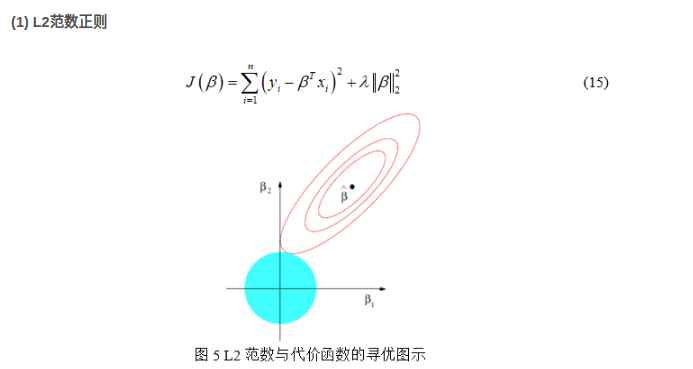
蓝色的是范数的解空间;红色的是损失函数的解空间.当两个空间相交时得到目标函数的一个解. 增加了正则化项后,随着r的不断增加,原始的解空间会被不断压缩, 如果选择的\(\lambda\), 可以将最优点压缩到\(\tilde{\beta}\),从而得到复杂程度最小的模型. L2范数和损失函数的交点处所得到的参数\(\beta\)可以无限小,但是不一定会等于0.

Lasso回归

拉索回归(lasso回归)本质上是针对线性回归问题引入了L1范数正则，通过缩减回归系数避免过拟合问题，其不同于L2范数，其可以将某些系数缩减为0即所谓的具备稀疏性(稀疏性的好处是简化计算、容易理解模型、减少存储空间、不容易出现过拟合等等．

L1范数罚有一个问题：由于|X|函数在0处不可导，故而直接使用最小二乘法、梯度下降法等方法均失效，但是由于其为第一类间断点中的可去间断点，可以通过补充该点的定义解决，通常，对于线性回归中的lasso回归可以采用近似的前向逐步回归，坐标轴下降法替代。

Ridge

岭回归本质上是针对线性回归问题引入了L2范数正则，通过缩减回归系数避免过拟合问题，最先用来处理特征数多于样本数的情况(高维小样本问题).

降维方法
-PCA
-

Logistic regression

总括

LR回归使用sigmoid函数，将线性模型 wTx 的结果压缩到[0,1] 之间，使其拥有概率意义。其本质还是一个线性模型，实现相对简单。

原理

逻辑斯蒂回归函数, 样本为正类的概率,样本为负类的概率. 样本的概率.
用极大似然函数求解, 损失函数是交叉熵, 最后求导等于普通的MSE求导的式子.

优化方法

梯度下降法实现相对简单，但是其收敛速度往往不尽人意。所以在LR回归的实际算法中，用到的是牛顿法，拟牛顿法（DFP、BFGS、L-BFGS）。

进一步优化--带正则化的LR

最大似然估计法没有考虑训练集以外的因素，很容易造成过拟合,为了解决过拟合问题，通过添加正则化项，控制模型的复杂程度。常用的有L1和L2正则化.
L1会是特征的权重系数为0，相当于是删除对应的特征；L2会保留原始的特征，但是特征的权重参数会很小。

QA

• 为什么使用正则化?
  ? 因为使用极大似然估计,模型会全力拟合数据,容易出现过拟合现象.

• 为什么一般使用L2正则化?
  ? 因为L2正则化只会使函数的某些参数缩小,降低这些参数的作用. 但是如果直接使用L1正则化会使参数直接为0, 会极大降低模型的效果. 所以一般我们选择更温和的L2正则化.

优点

1. 计算代价不高，对时间和内存需求较小,很适合大数据.(推荐系统)
2. 使用梯度下降的优化算法可以用于分布式系统，并且还有在线算法实现，用较少的资源处理大型数据。(推荐系统)
3. LR对于数据中小噪声的鲁棒性很好，并且不会受到轻微的多重共线性的特别影响。（严重的多重共线性则可以使用逻辑回归结合L2正则化来解决，但是若要得到一个简约模型，L2正则化并不是最好的选择，因为它建立的模型涵盖了全部的特征。）

缺点

sigmoid函数的缺点。预测结果呈“S”型，因此从log(odds)向概率转化的过程是非线性的，在两端随着?log(odds)值的变化，概率变化很小，边际值太小，slope太小，而中间概率的变化很大，很敏感。导致很多区间的变量变化对目标概率的影响没有区分度，无法确定阀值。

这段出现错误的原因是LR的优化方式是\(y_i-\tilde{y_i}，使用梯度下降法就得到结果，根本和sigmoid函数没有关系\)

1. 不适应数据缺失，特征空间很大的数据
2. 因为w表示各个特征的权重,一旦特征过多,很容易过拟合.
   过拟合的真正原因是使用极大似然估计,没有考虑除了当前数据之外的数据,所以容易过拟合.

应用

在CTR预估问题的发展初期，使用最多的方法就是逻辑回归(LR)，LR使用了Sigmoid变换将函数值映射到0~1区间，映射后的函数值就是CTR的预估值。LR属于线性模型，容易并行化，可以轻松处理上亿条数据，但是学习能力十分有限，需要大量的特征工程来增加模型的学习能力。但大量的特征工程耗时耗力同时并不一定会带来效果提升。因此，如何自动发现有效的特征、特征组合，弥补人工经验不足，缩短LR特征实验周期，是亟需解决的问题。FM模型通过隐变量的方式，发现两两特征之间的组合关系，但这种特征组合仅限于两两特征之间，后来发展出来了使用深度神经网络去挖掘更高层次的特征组合关系。但其实在使用神经网络之前，GBDT也是一种经常用来发现特征组合的有效思路。

用LR做点击率预估时，通常将连续特征离散化，并对离散化的特征进行One-Hot编码，最后对特征进行二阶或者三阶的特征组合，目的是为了得到非线性的特征,这样做的优势有以下几点:

• 稀疏向量容易计算
• 离散化的特征鲁棒性很强

GBDT和LR的融合方案，FaceBook的paper中有个例子：

图中共有两棵树，x为一条输入样本，遍历两棵树后，x样本分别落到两颗树的叶子节点上，每个叶子节点对应LR一维特征，那么通过遍历树，就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1的。举例来说：上图有两棵树，左树有三个叶子节点，右树有两个叶子节点，最终的特征即为五维的向量。对于输入x，假设他落在左树第一个节点，编码[1,0,0]，落在右树第二个节点则编码[0,1]，所以整体的编码为[1,0,0,0,1]，这类编码作为特征,输入到LR中进行分类。特征的物理意义是它使用了第1个和最后一个特征,这样实际上就是将不同的特征做特征组合.选中叶子越多组合包含的特征的个数越多.

针对商品的长尾现象:
针对ID建一种树,针对非ID建一种,结合两种树的结果来使用.

QA:

• 为什么要使用集成的决策树模型，而不是单棵的决策树模型?
  ? 一棵树的表达能力很弱，不足以表达多个有区分性的特征组合，多棵树的表达能力更强一些。可以更好的发现有效的特征和特征组合.

• 为什么建树采用GBDT而非RF?
  ? RF也是多棵树，但从效果上有实践证明不如GBDT。且GBDT前面的树，特征分裂主要体现对多数样本有区分度的特征；后面的树，主要体现的是经过前N颗树，残差仍然较大的少数样本。优先选用在整体上有区分度的特征，再选用针对少数样本有区分度的特征，思路更加合理，这应该也是用GBDT的原因。

• 除了GBDT+LR的方案,还有哪些思路可以挖掘有效的特征组合?
  ? GBDT+FM

• 通过GBDT 映射得到的特征空间维度如何？
  ? GBDT树有多少个叶子节点，通过GBDT得到的特征空间就有多大。如下图4一颗树，一个叶子节点对应一种有区分性的特征、特征组合，对应LR的一维特征。这颗树有8个叶子节点，即对应LR 的8维特征。估算一下，通过GBDT转换得到的特征空间较低.即使在树多的情况下, 叶子节点的数量依然不多,所以通过GBDT得到的特征数量依然很少.

LR VS 最大熵模型

简单粗暴的说：逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应为二类时的特殊情况，也就是说，当逻辑回归扩展为多类别的时候，就是最大熵模型。
最大熵原理：学习概率模型的时候，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。

LR VS SVM

目标函数、优化方法、具体实现

SVM

总括

假设问题是二分类器，就是在特征空间中寻找使正类负类间隔最大的超平面的线性分类器。根据输入的数量类型不同，得到分类器也不同。

    A[间隔最大化的超平面] --> B{样本是否线性可分}
    B --> |线性可分| D[间隔最大化]
    B --> |近似线性可分| E[引用松弛变量]
    B --> |无法线性可分| F[核技巧]
    D --> G[线性分类器]
    E --> G
    F --> H[非线性分类器]

原理

线性可分

间隔-拉格朗日解决凸优化问题-对偶问题(求优化下界)-求导

近似可分

加入松弛项，求导过程

核函数

1. 线性核 \(K(x,x')=x^Tx'\) (相当于没用)

优点：用于线性可分，对一般的数据效果还行；没参数，速度快
缺点：只适合特征多，样本少或者特征数量和样本数量差不多的情况，可以充分拟合数据特征。尤其是特征数量非常多的时候，linear优势非常明显。

2. 高斯核 \(K(x,x')=e^{(-\frac{(x-x')^2}{\gamma^2})}\)

优点：线性不可分，效果好；参数只有一个；适合特征<样本的情况。
缺点：原始空间映射到无线维，\(\gamma\) 过大会使特征数量过多，特征的权重衰减到很小，相当是低维空间；\(\gamma\) 选的很小，可以将任意数据转成线性可分，但是可能导致过拟合；如果过高维度，计算慢；效果高度依赖\(\gamma\)参数。

RBF核：分类结果非常依赖于参数。有很多人是通过训练数据的交叉验证来寻找合适的参数，不过这个过程比较耗时。我个人的体会是：使用libsvm，默认参数，RBF核比Linear核效果稍差。通过进行大量参数的尝试，一般能找到比linear核更好的效果。至于到底该采用哪种核，要根据具体问题，有的数据是线性可分的，有的不可分，需要多尝试不同核不同参数。如果特征的提取的好，包含的信息量足够大，很多问题都是线性可分的。当然，如果有足够的时间去寻找RBF核参数，应该能达到更好的效果。

3.多项式核 \(K(x,x')=(\gamma\cdot x^Tx' + coef0)^{degree}\)

优点：degree过大过拟合，过小没效果；时间快
缺点：参数多

4.sigmoid核 \(K(x,x')=tanh(\gamma\cdot x^Tx' + coef0)\)

没有用过

SMO算法

只保留两个参数 -> 只保留一个参数 -> 求导 -> \(new1+new2=old1+old2\), \(E(x_i)=f(x_i)-y_i\) \(v_j=\sum_{j=3}^{N}{\alpha_jy_jK(x_i,x_j)}\) -> 式子整个只留下了\(\alpha_i\)

优点

• SVM有多种核可以选择，可以处理各种非线性问题（条件是选对核函数）。
• SVM 的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,而不是样本空间的维数,这在某种意义上避免了“维数灾难”
• 支持向量样本集具有一定的鲁棒性

缺点

• SVM算法对大规模训练样本难以实施.因为SVM用二次规划求解支持向量，数目很大，时间消耗很大,大多数情况准确率都比LR要高，但是模型较大，训练效率低。
• 用SVM解决多分类问题存在困难,经典的算法只给出了二分类的情况

QA
SVM模型为什么比其他模型更好？

Random Forest

总括

是一种典型的bagging集成算法。
工作流程是：针对样本，会随机抽取不同的样本和特征训练不剪枝的CART树，一直训练到达到预定义的基分类器个数。对于输出，针对分类问题，预测结果是各个基分类器的投票，针对回归问题，预测结果是各个分类器的输出结果的平均值。

模型评价 (准确率 \时间 \空间 \模型复杂程度 \过拟合 \噪声影响 \是否可并行化 \调参)

1. 准确率: 相比GBST,它默认参数的效果不错,可以很好地作为baseline模型
2. 时间: 时间复杂度主要取决于数据集的复杂程度,如果数据集很复杂的话, 需要100-200棵树, 如果不复杂的话,一般10-100棵树就好
3. 空间:空间复杂度因为需要训练大量的树, 所以很耗内存.
4. 模型复杂度: 模型很简单
5. 过拟合: 每次采取部分的样本, 所以在树的深度和树的数量不过分的情况下, 是不会出现过拟合现象的.
6. 噪声影响: 采取随机采取的方式,不一定会采到特征, 所以抗噪声能力很好
7. 是否可并行化: 因为树模型之间无关联,所以可以并行化.
8. 调参: 树的棵树, 层数, 特征数量, 叶子节点的最少样本数量, 内部节点的最少样本数量,

缺点

1. 耗时:每个基分类器的准确率不是很高，所以要求有大量的基分类器才能取得良好的效果，一般是100-200，整体的训练时间很长。
2. 耗内存

QA:

• 为什么RF不用后剪枝,但是实现了预剪枝?
  ? 方差和偏差的角度
• 为什么要用随机采取样本和特征的方式?
  ? 优点:样本数量,模型差异化;
  ? 缺点:欠拟合(配合强分类就可以效果很好)
• 为什么可以并行化?
  ? 模型之间没有关联
• RF使用的是什么树?
  ? 可以是分类树也可以是回归树
• RF对输入数据有什么要求吗?
  ? RF可以直接用原始数据, 也就是说不需要数据预处理

调参小结

1. 相比GBDT的默认输出，RF的默认参数要好一些。
2. 先调节分类器个数从10:200的范围内挑，但是一般数据较小的话，10:100就可以了
3. 在调节最大深度，调节最大深度要和内部节点的最小样本数量一起调，最大深度的范围[3-20]，节点的最小样本数量范围[50,200]
4. 在调节内部节点的最少样本数量和叶子节点的最少样本数量，范围分别是[80,150],[10,50]
5. 最后调节特征数量，一般是[0.5,0.8]

bagging 和Boosting的区别:

Bagging:

1. 随机抽取样本和特征训练分类器.
2. 强模型(偏差小,方差大).

Boosting:

1. 迭代构建一系列分类器, 每次分类都将上一次分错的样本的权重提高.
2. 弱模型(偏差大,方差小)

QA:

• 为什么Bagging模型使用强模型?
  ? 整体模型的期望近似等于基模型的期望,也就是说整体模型的最后偏差和每棵树的偏差相等.整体模型的方差小于基模型的方差,随着模型数量的增多,整体模型的方差减小. 但是当基模型的数量增加到一定程度的时候方差是无法继续减小了.
• 为什么Boosting 使用弱模型?
  ? Boosting模型都针对分错的样本进行优化,所以每个基分类器的准确率是能够得到保证的. 如果就需要考虑方差. 如果是强模型的话,基分类器的个数越多,方差越大. 但是弱分类的方差会稍微比强基分类器的方差小一点.

ADAboost

总括

Adaboost算法是boosting算法之一,会更多的关注上一次分类器误分的样本。
工作机制是：将样本初始赋一个权重，用这些样本训练一个基分类器，根据这个基分类器对样本的表现调整样本的权重，如果样本分类器正确的话，权重降低，如果样本分类错误的话，权重上升。再用调整过的权重的样本训练基分类器，反复学习知道分类器个数达到指定个数。对预测样本的输出是结合所有基分类器的权重输出。最小化目标是指数损失函数。

模型评价(准确率,时间,空间,模型复杂度,过拟合,抗噪声,是否可并行化,调参)

1. 准确率: 模型的实际效果一般, 我自己做多分类的时候选用ADAboost作为二分类效果并没有很好.
2. 时间: 在小数据上, 模型选用简单的树模型, 有深度限制并且不需要大量的树, 所以时间很快
3. 空间: 需要树的数量少, 消耗的空间也就小
4. 模型复杂度:模型稍微优点复杂,主要是样本的权重调整计算公式上.
5. 过拟合: 周志华的Margin理论：
   泛化错误（泛化错误可理解为测试错误） < 训练错误 + 学习算法容量相关项 (1)
   泛化错误 < 训练Margin项 + 学习算法容量相关项 (2)　Margin:对的信心
   泛化错误 < 训练Margin的最小值 + 学习算法容量相关项 (3) 信心最不足的那个
   泛化错误 < 训练Margin的某个值 + 学习算法容量相关项 (3) 某个信心值
   现实的经验例子也证明了这一点，AdaBoost不容易过拟合。随着Margin变大，泛化误差会收敛
6. 抗噪声: 容易受到噪声的污染
7. 是否可并行化: 模型不可并行化, 特征可以并行化
8. 调参: 树的个数和缩减率,调参是比较容易的.

优点

1. 不改变训练数据，只是改变训练样本的权重分布。

缺点

1. 过分关注容易错误分类的样本，如果错误分类样本是噪声点，那么算法容易产生过拟合。
2. 是个二分类算法。

GBDT

总括

是一种迭代的决策回归树算法,也是一种典型的Boosting算法。
原始的工作流程是：初始化**CART回归树**，针对每个样本计算残差，将这个残差作为新的真实值，用新的数据去训练下一个CART树。不断迭代直到决策树的个数达到预定义的数量停止，结合所有基分类器的输出作为最后结果的输出。(现在已经有了一个模型F,但是觉得它做的不够好,希望在他的基础上得到一个更好的模型,所以就新加一个模型h(x), 这样最后得到的总结果就是F(x)+h(x))
用缩减率改进的工作流程:认为每次走一小步比走一大步更能获得好的效果，更能防止过拟合。工作流程：仍然以残差作为学习目标，但是每次只是用step*残差逐步逼近目标，step一般是0.001-0.1.和神经网络的的学习率是一样的。本质上缩减是给每棵树设置了一个权重系数。所以能取得良好的效果。

QA:

• 为什么要使用回归决策树?
  GBDT的核心在于累加所有树的结果.
  ?分类树用于分类, 最后的结果是类别, 如果男女, 这样累加类别是没有意义的.
  ?回归树用于预测数值, 最后的结果是实数, 累加起来依然是具有实际意义的.

• 分类树和回归树的区别是什么?
  ? 分类树使用信息增益/信息增益率/基尼指数来划分节点, 中间会穷举所有特征的所有阈值, 最后选择一个合适的划分特征,最后根据叶子节点的投票确定预测样本的类别
  ? 回归树使用最小化均方差划分节点, 中间会穷举所有特征的所有划分点, 最后根据叶子节点的样本均值作为预测样本的回归预测值.

• 为什么将残差做为真实值？
  ? GBDT算法本质是一种加法模型，它的目标函数是MSE，导数是\(\tilde{y_i}-y_i\)。所以残差就是下一步的最优化的反方向。
  ? 每一步的残差计算其实变相的增大了分错样本的权重，而已经分对的样本则都趋向于0。这样后面就更加专注于那些分错的样本。

模型评价(准确率,时间,空间,模型复杂度, 过拟合,抗噪声, 是否可并行化,调参)

准确率: 针对分类和回归任务都有很好的性能
时间: 小型的数据上,不需要训练大量的树, 模型也比较简单, 时间复杂度较小.但是在大数据上, 不能用类似 mini batch 的方式来训练，需要对数据进行无数次的遍历。如果想要速度，就需要把数据都预加载在内存中，但这样数据就会受限于内存的大小；如果想要训练更多的数据，就要使用外存版本的决策树算法。虽然外存算法也有较多优化，SSD也在普及，但在频繁的 IO 下，速度还是比较慢的。
空间: 也较小.
模型复杂度: 模型最后的公式很简单
过拟合: 和ADAboost的过拟合效果差不多.
抗噪声: 对异常值很敏感
是否可并行化:主要是在生成每一颗树的时候：并行的计算最佳分裂点。每个节点负责一些特征.
调参:树的棵树,缩减率, 采样率(不放回采样), 损失函数

RF VS. ADABoost VS. GBDT

工作流程,特点,使用场景
备注：如果针对为处理的数据，可以先用随机森林测试看一下大致的结果，然后在用GBDT继续优化。

XGBoost

总括：是GBDT的改进版，主要改进在两点：目标函数加入正则化项和损失函数使用。之前的GBDT残差是MSE损失函数的一阶导数，现在使用其他损失函数，并且加入其二阶导数的信息。正则化项是CART回归树的生成和叶子节点的数量和叶子节点的得分有关.

优化

1. 近似分割算法
   之前存在的问题是: 树分裂节点的时候需要每个特征的每个划分点,不断尝试,这样会导致计算量非常大。
   解决方案:使用特征的分位点将整个特征区间划分为多个段，所有特征值将进入对应分段，接着对每个桶内的样本统计值G、H进行累加统计，最后在这些累计的统计量上寻找最佳分裂点.(本质就是用分位点作为特征抽取量,只用这些数据就可以计算出近似最优点).
   选取切分点的算法是:加权的分位数算法.,以二阶梯度加权.
   所以直方图算法是牺牲了一定的切分准确性而换取训练速度和节省内存空间的算法.

为什么使用二阶梯度作为加权?
从损失函数的角度推导, 可以推出以\(-frac{g_i}{h_i}\)作为标签, \(h_i\)为权重的平方损失,因此用\(h_i\)作为加权.

1. 处理缺失值
   实际运用中，输入很可能是稀疏的。有很多种可能造成数据是稀疏的：1) 数据中的缺失值； 2）较多的0值；3) 类似one-hot的特征工程。之前处理方式存在的问题是:树分裂选择特征时候,直接忽略这些特征.
   对于这些缺失值，xgboost将样本分类到默认分支上去，而默认分支是提出的non-missing value算法学习到的。
   选择特征的时候会考虑有missing的特征. 具体方法是: 会忽略该特征值为missing的样本,只统计该特征值为non-missing的样本. 同时考虑将该特征值为missing的样本分为左子树和右子树的情况,选择特征增益大的方向进行分裂.

使用了该方法，相当于比传统方法多遍历了一次，但是它只在非缺失值的样本上进行迭代，因此其复杂度与非缺失值的样本成线性关系。在Allstate-10k数据集上，比传统方法快了50倍:

1. 内存优化
   之前存在的问题是: 确定最优分割点时要排序所有的属性值,这个很耗时间
   解决的方式:在训练之前就进行预排序,然后保存成block数据，存储数据的内容，行号，列号。所以遍历特征的取值的时候只要遍历values数组就可以了,只有反复用这个数据就可以了.

2. 多线程并行
   XGBoost的并行是发生在树向下分裂节点的时候. 它会把所有的数据放在一个共享内存中, 分裂的时候,将特征分成多组,每个线程计算一组特征,底层调用的是用C语言的OpenMP库.
   同时, 针对内存无法放下的数据问题, 统一的多节点的API借口正在开发中,未来可能会使用
   C++的后端+Yarn分布式系统.

模型评价(准确率,时间,空间,模型复杂度,过拟合,抗噪声,是否可并行化,调参)

• 准确率: 可以处理分类和回归问题, 但是完全依靠调参才能取得好的效果
• 时间: 速度很快
  • 需要树的棵树较少
  • 减少了预排序的次数
  • 优化找到分裂最优点的方式
• 内存: 用了block数据结构,剩空间
• 模型复杂度: 用了损失函数的一阶导和二阶导信息, 同时加入了节点的样本个数和节点得分作为正则化项
• 过拟合: 也是用了缩减率和采样率防止过拟合
• 抗噪声: 使用了行采样和列采样,所以就对噪声不敏感.
  • 训练树的子样本比例. 设置成0.5 意味着XGBoost随机搜集一般的样本来训练树
  • 训练特征的特征比例.
  • 每个级别中每个拆分的列的子样本比例. 指的应该是树分裂时选择的候选特征的比例.
• 是否可并行化: 分裂特征并行化
• 调参:0
  • 通用参数: 树的棵树,深度, 叶子节点的最小样本数量, 采样比例, 缩减比例
  • booster参数: 目标函数,损失函数,多线程的数量

　优点

• 不仅支持决策树作为基分类器，还支持线性分类器
• 用到了损失函数的二阶泰勒展开，因此与损失函数更接近，收敛更快
• 在代价函数中加入了正则项，用于控制模型复杂度。正则项里包括了树的叶子节点个数和叶子结点输出值的L2范数，可以防止模型过拟合
• 内置了交叉验证。节省验证集
• 可以随时保存模型，下一次运行在上一次保存的模型基础上开始
• 良好的可拓展性和接口，适合常见的任何一种语言

QA:

• 为什么XGBoost使用损失函数的一阶导和二阶导?
  ? 二阶偏导相当于找到了一阶导数的下降方向, 会使梯度下降的更快, 收敛的更快.

• 为什么可以使用近似搜索算法?
  ? 虽然使用直方图会降低模型的准确率,但是决策树本身就是弱模型, 分割点不是很精确对最后的结果影响不大,
  ?较粗的分割点也有正则化的效果, 可以有效防止过拟合.
  ?同时梯度提升的框架对每次模型的结果的要求不是很高!

• 为什么XGBoost使用泰勒展开?
  ? 使用泰勒展开可以在不确定损失函数的情况下分析算法优化, 本质上是把损失函数的选取和模型的优化分开了, 是一种去耦合的方式. 增加了XGBoost的适用性.

• 为什么机器学习比赛中很少用使用SVM？
  ? SVM的输入数据适合数值型
  ? XGBoost模型的良好可扩展性

• 为什么XGBoost适合比赛?
  ?深度神经网络通过不同step的网络可以对时空信息建模，就很适合图像, 声音, 文字等带有时序特质的数据.
  ?基于树模型的XGBoost则能很好地处理表格数据，同时模型的可解释性、输入数据的不变性、更易于调参等特质更适合数值型数据.

• 为什么XGBoost用很低的深度就可以学到很好的精度,一般6就很高了。但是DecisionTree/RandomForest的时候需要把树的深度调到15或更高，这是为什么？
  ?RF是Bagging算法，同时在基分类器上采用了随机抽取样本和特征的方式，使得每个基分类器的精度下降，所以只有当决策树的深度足够深的时候，才能提高基分类器的精度。
  ?XGBoost是Boosting算法，每个决策树都在之前决策树的基础上进一步提高了预测精度，所以就不需要很深的树就可以实现好的效果，反之选择深度小的，可以防止过拟合。

• 如果用其他模型换掉XGBoost的，哪种模型（知识广度）
  ? 最好的替代品是LightGBM
  ? 针对分类任务: 基础的SVM, LR
  ? 针对回归任务: 基础的Lasso, 岭回归

缺点

目前没发现

XGBoost的调参经验

确定线性模型还是树，树模型（常用的）
确定object学习目标：线性回归，逻辑回归，二分类的逻辑回归（输出是概率还是类别），多分类（输出是概率还是类别）
调节的参数：基分类器的数量，每棵树的深度，内部节点分裂的最小样本数量和叶子节点的最小样本数量。学习率，使用的特征数量，使用的样本数量。网格搜索，先是大范围再小范围。

LightGBM (基于GBDT算法)

优化

1. 直方图算法
   和XGBoost的优化是策略是一样的.
   流程:
   - 首先,对于每个特征建立一个离散值的划分区间(桶), 其中保存了所有样本的二阶导数之和和样本个数.
   - 分配所有的样本到每个桶中
   - 遍历所有的桶,计算以当前桶作为分割点, 所有左边桶的所有样本的梯度和,所有右边桶的所有样本的所有梯度和(由父节点的梯度和和左边的梯度相减得到)
   - 带入公式\(Loss=\frac{s_{L}^{2}}{n_L}+\frac{s_{R}^{2}}{n_L}-\frac{s_{p}^{2}}{n_p}\), 计算增益
   - 选择增益最大的桶的特征和特征值作为分裂的最优特征.
2. 直方图差加速
   一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到, 在分裂节点的时候, 计算玩所有左孩子的直方图之后, 直接用父节点的直方图-左孩子的直方图就可以得到右孩子的直方图.
3. 带深度限制的叶子生长策略
   之前向下生长树的时候, 同时分裂同一层叶子, 容易进行多线程, 但是存在的问题不加区分的对待同一层的叶子,如果叶子的分裂增益很低没必要继续分裂.
   所以为了解决这个问题, 在生长的时候,每次从当前叶子中找到分裂增益最大的一个叶子进行分裂.
   缺点是可能找出深度很深的树,容易过拟合,所以LightGBM做了最大深度限制,保证高效率的同时防止过拟合.
4. 支持类别属性特征（不需要one hot）
5. 特征并行
   ? 在不同的机器在不同的特征集合上分别寻找最优的分割点, 然后再机器间同步最优的分割点.
6. 数据并行
   ? 让不同的机器先在本地构造直方图, 然后进行全局的合并,然后在合并的直方图上寻找最优的分割点.

QA:

• XGBoost的近似搜索算法和LightGBM的直方图算法有什么区别?
  ? XGBoost的近似搜索算法是保存所有样本的二阶梯度, 用分位数确定划分方法,他的分割点是可以直接通过计算总的样本梯度和和分位数点得到的.
  ? LightGBM算法是将所有样本放进对应的桶中,并以当前桶作为划分点, 计算左右桶的最大增益.它的最优点是遍历所有的桶才能得到的.

• 为什么LightGBM也使用了直方图,但是速度依然比较慢?
  ?模型的其他优化: LightGBM除了直方图优化,还有数据的垂直分割,水平分割等优化方式
  ? 直方图算法的实现有两种:1. 全局构造,在树的构造过程中只建立一次直方图, 每次分裂都从缓存的直方图中寻找分裂点. 2. 局部构造, 每次树分裂到一层的时候就建立一次直方图. 但是XGBoost使用的是局部构造的方式, 所以速度会较慢.

LR、SVM、RF、GBDT、XGBoost和LightGbm比较

原文：https://www.cnblogs.com/x739400043/p/10098659.html