最优化算法

1、无约束最优化问题

求解此问题的方法方法分为两大类：最优条件法和迭代法。

2、最优条件法

我们常常就是通过这个必要条件去求取可能的极小值点，再验证这些点是否真的是极小值点。当上式方程可以求解的时候，无约束最优化问题基本就解决了。实际中，这个方程往往难以求解。这就引出了第二大类方法：迭代法。

最优条件法：最小二乘估计

3、迭代法

（1）梯度下降法（gradient descent），又称最速下降法（steepest descent）

梯度下降法是求解无约束最优化问题的一种最常用的方法。梯度下降法是迭代算法，每一步需要求解目标函数的梯度向量。

必备条件：函数f(x)必须可微，也就是说函数f(x)的梯度必须存在

优点：实现简单

缺点：最速下降法是一阶收敛的，往往需要多次迭代才能接近问题最优解。

 算法A.1（梯度下降法）

输入：目标函数f(x)，梯度函数g(x)=▽f(x)，计算精度ε；

输出：f(x)的极小点x*

 总结：选取适当的初值x⁽⁰⁾,不断迭代，更新x的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新x的值，从而达到减少函数值的目的。λ_k叫步长或者学习率。

泰勒公式：

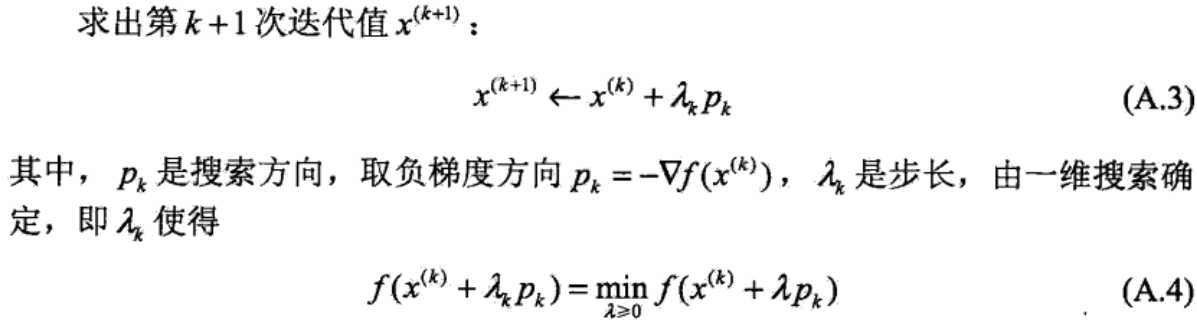
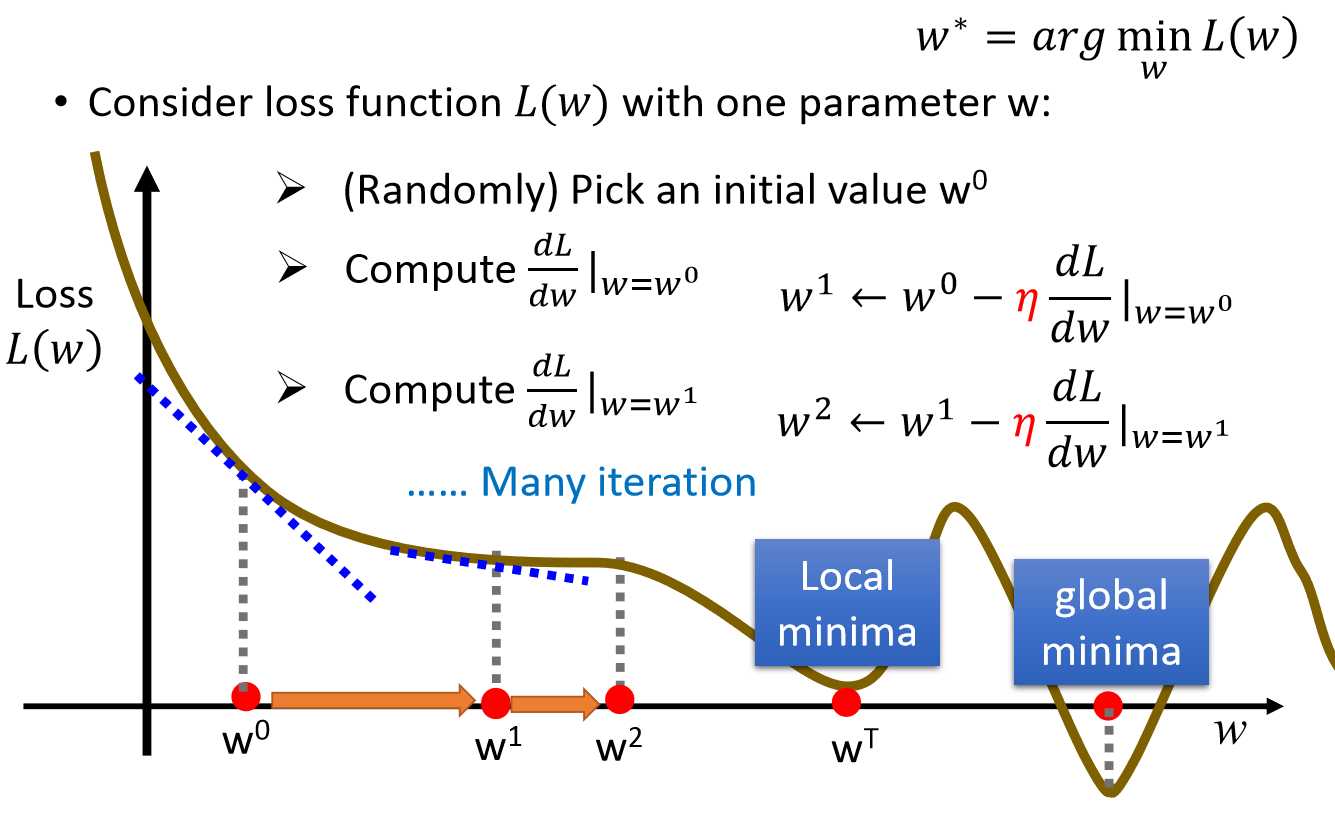
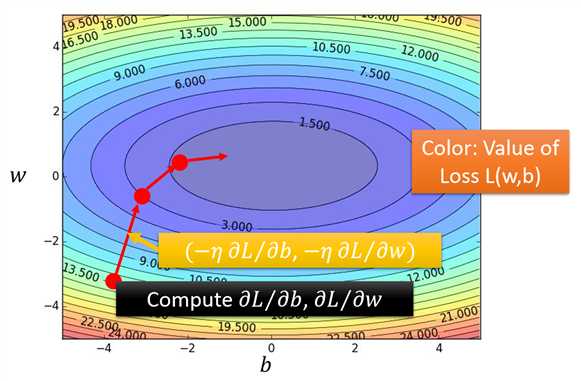
当f(x)的形式确定，我们可以通过求解这个一元方程来获得迭代步长λ。当此方程形式复杂，解析解不存在，我们就需要使用“一维搜索”来求解λ了。一维搜索是一些数值方法，有0.618法、Fibonacci法、抛物线法等等，这里不详细解释了。

在实际使用中，为了简便，也可以使用一个预定义的常数而不用一维搜索来确定步长λ。这时步长的选择往往根据经验或者通过试算来确定。步长过小则收敛慢，步长过大可能震荡而不收敛。如下图：

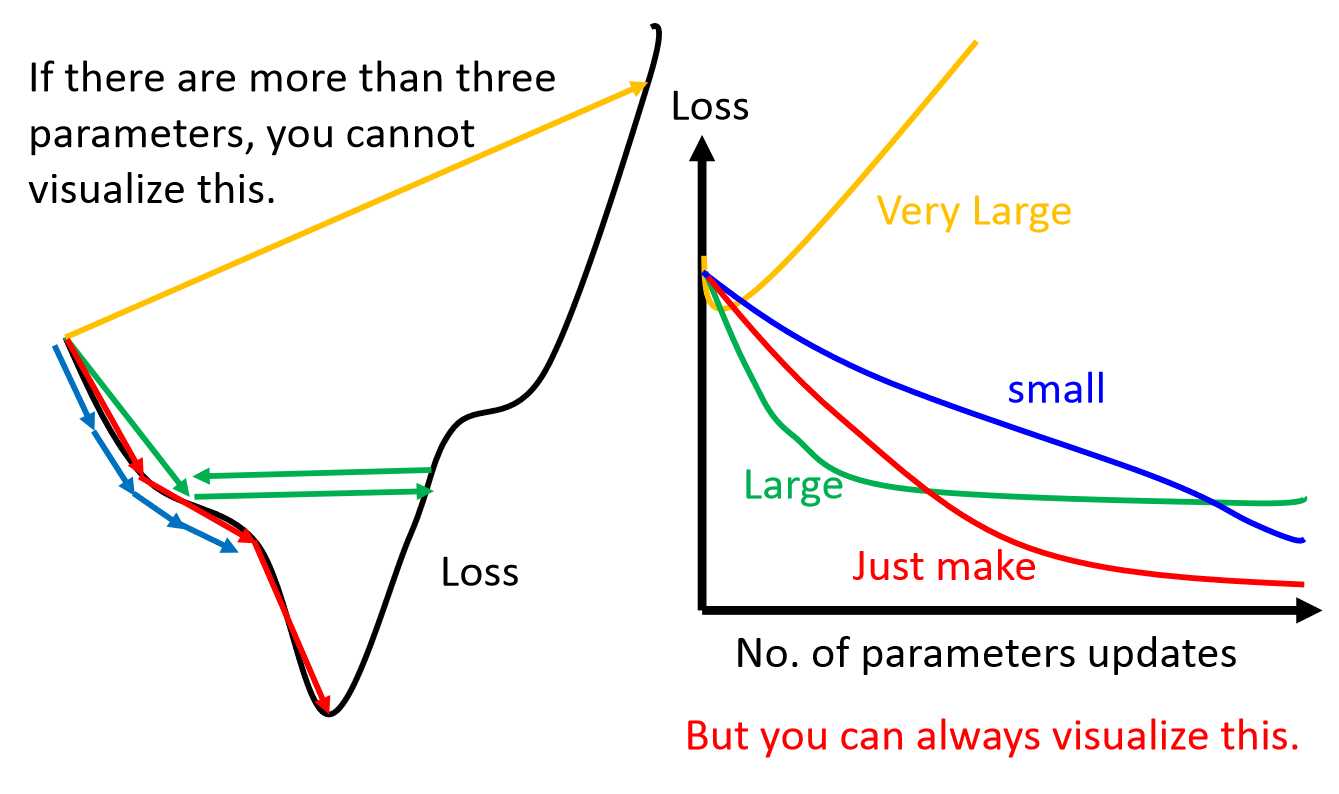
当目标函数是凸函数时，梯度下降法的解是全局最优解。但是，一般情况下，往往不是凸函数，所以其解不保证是全局最优解。梯度下降法的收敛速度也未必是最快的。

转载：https://blog.csdn.net/hanlin_tan/article/details/47376237 

参考：李航《统计学习方法》、李宏毅《机器学习》

最优化算法

原文：https://www.cnblogs.com/Christina-Notebook/p/10111516.html