题目：非负整数a,b使得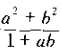
为整数，求证这个整数必是某一整数的平方。（1988年第29届国际数学奥林匹克竞赛试题）
证明：设k=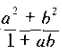
，k为非负整数
1°a=b
k=2a²/(1+a²)=2-2/(1+a²) 故k∈[0,2) ，所以k=0或1
故k是平方数；
2°不妨设a>b>=0
若b=0，k=a²，故k是平方数；
a>b>0时，讨论二次方程x²-kbx+b²-k=0
已知其中一个根是a，设另一个根是a1
韦达定理：a+a1=kb ① 故a1为整数
a a1=b²-k ②
②可知a1 = (b²-k)/a < b²/a = b/a *b < b
假设a1<0 ， 0=a1²+b²-a1 bk-k >= a1²+b² > 0 推出矛盾，故a1>=0
若a1=0，②可知k=b²，故k是平方数；
a1>0，b>a1>0 ①②可知k=(a1²+b²)/(1+a1 b)
重复上述过程，可以找到整数b1，满足b>a1>b1，并使k=(a1²+b1²)/(1+a1 b1)
又回到了原来的情况，这时候有a>b>a1>b1，显然不能无限进行下去，故必然有一个ai=0或bi=0
故k是平方数。
原文：http://www.cnblogs.com/CQBZOIer-zyy/p/3885540.html